(本小题满分12分)

设函数.

(1)若函数的图象在点处的切线为直线l，且直线l与圆相切，求a的值；

(2)当时，求函数f(x)的单调区间．

本小题满分12分）

今有一长2米宽1米的矩形铁皮，如图，在四个角上分别截去一个边长为x米的正方形后，沿虚线折起可做成一个无盖的长方体形水箱(接口连接问题不考虑)．

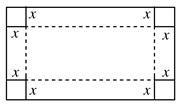
(Ⅰ)求水箱容积的表达式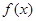，并指出函数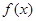的定义域；

(Ⅱ)若要使水箱容积不大于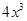立方米的同时，又使得底面积最大，求x的值．

（本小题满分12分）

函数f(x) = sinωxcosωx + sin²ωx +  ,其图像相邻两条对称轴之间的距离为 ．

（Ⅰ）求ω的值；

（Ⅱ） 若A为△ABC的内角，且f  = ，求A的值.

 (本小题满分12分)  已知函数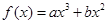的图像经过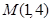点，曲线在点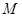处的切线恰好与直线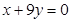垂直．

（I）求实数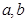的值；

（Ⅱ）若函数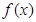在区间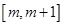上单调递增，求实数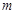的取值范围．

(本小题满分12分)已知函数f(x)＝x³＋x²－2.

(1)设{a_n}是正数组成的数列，前n项和为S_n，其中a₁＝3.若点(a_n，a_n＋1²－2a_n＋1)(n∈N^*)在函数y＝f′(x)的图象上，求证：点(n，S_n)也在y＝f′(x)的图象上；

(2)求函数f(x)在区间(a－1，a)内的极值．