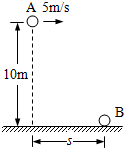（2010?宝山区一模）如图所示，某人在离地面高10m处，以5m/s的初速度水平抛出A球，与此同时在离A球抛出点水平距离s处，另一人竖直上抛B球，不计空气阻力和人的高度，试问：要使B球上升到最高点时与A球相遇，则（g=10m/s²）
（1）B球被抛出时的初速度为多少？
（2）水平距离s为多少？

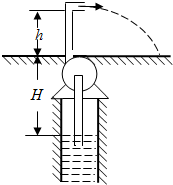（2012?宝山区二模）节水喷灌系统已经在我国很多地区使用．某节水喷灌系统如图所示，喷口距离地面的高度h=1.8m，能沿水平方向旋转，水可沿水平方向喷出，喷水的最大速率v₀=15m/s，每秒喷出水的质量m₀=4.0kg．所用的水是从井下抽取的，井中水面离地面的高度H=1.95m，并一直保持不变．水泵由电动机带动，电动机电枢线圈电阻r=5.0Ω．电动机正常工作时，电动机的输入电压U=220V，输入电流I=4.0A．不计电动机的摩擦损耗，电动机的输出功率等于水泵所需要的最大输入功率．水泵的输出功率与输入功率之比称为水泵的抽水效率．（计算时π可取3，球体表面积公式s=4πr²）
（1）求这个喷灌系统所能喷灌的最大面积s；
（2）假设系统总是以最大喷水速度工作，求水泵的抽水效率η；
（3）假设系统总是以最大喷水速度工作，在某地区需要用蓄电池将太阳能电池产生的电能存储起来供该系统使用，根据以下数据求所需太阳能电池板的最小面积s_min．
已知：太阳光传播到达地面的过程中大约有30%的能量损耗，太阳辐射的总功率P0=4×1026W，太阳到地球的距离R=1.5×10¹¹m，太阳能电池的能量转化效率约为15%，蓄电池释放电能的效率约为90%．