
题目列表(包括答案和解析)
过双曲线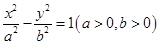 的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于______.
的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于______.
过双曲线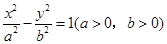 的左焦点且垂直于x轴的直线与双曲线相交于
的左焦点且垂直于x轴的直线与双曲线相交于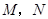 两点,以
两点,以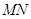 为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于 .
为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于 .
过双曲线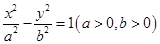 的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于______.
的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于______.
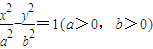 的左焦点且垂直于x轴的直线与双曲线相交于M,N两点,以MN为直径的圆恰好过双曲线的右焦点,则双曲线的离心率等于 .
的左焦点且垂直于x轴的直线与双曲线相交于M,N两点,以MN为直径的圆恰好过双曲线的右焦点,则双曲线的离心率等于 .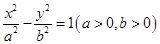 的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于______.
的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于______.一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,恰有一项是符合题目要求的.
(1) 函数 =lg(x2-2x-3)的定义域是集合M,函数
=lg(x2-2x-3)的定义域是集合M,函数 =
= 的定义域是集合P,则P∪M等于 ( A )
的定义域是集合P,则P∪M等于 ( A )
(A)(-∞,-1)∪[1,+∞) (B)(-∞,-3)∪[1,+∞)
(C)(-3,+∞) (D)(-1,+∞)
(2) 在等比数列{an}中,a1=3,a6=24,则a16等于 ( D )
(A)864 (B)1176 (C)1440 (D)1536
(3) 直线 关于直线
关于直线 对称的直线方程是 ( A )
对称的直线方程是 ( A )
(A) (B)
(B)
(C) (D)
(D)
(4) 若平面α⊥平面β,l,m,n为两两互不重合的三条直线, ,α∩β=l,且m⊥n,则 ( D )
,α∩β=l,且m⊥n,则 ( D )
(A) 且n∥l (B)
且n∥l (B) 或n∥l
或n∥l
(C) 且
且 (D)
(D) 或
或
(5)
△ABC中,若 ,则△ABC一定是 ( C )
,则△ABC一定是 ( C )
(A)锐角三角形 (B)钝角三角形 (C)直角三角形 (D)等腰三角形
(6) 函数 =
= 在区间(-2,2)上 ( B )
在区间(-2,2)上 ( B )
(A)单调递增 (B)单调递减
(C)先单调递增后单调递减 (D)先单调递减后单调递增
 (7)
如图,已知A,B,C是表面积为48π的球面上的三点,
(7)
如图,已知A,B,C是表面积为48π的球面上的三点,
AB=2,BC=4,∠ABC=60°,O为球心,则二面角
O-AB-C的大小为 ( D )
(A) (B)
(B)
(C)arccos (D)arccos
(D)arccos
(8) 一圆形纸片的圆心为O,点Q是圆内异于O点的一定点,点A是圆周上一点,把纸片折叠使点A与点Q重合,然后抹平纸片,折痕CD与OA交于P点,当点A运动时点P的轨迹是 ( A )
(A)椭圆 (B)双曲线 (C)抛物线 (D)圆
(9) 方程 的解共有 ( C )
的解共有 ( C )
(A)1个 (B)2个 (C)3个 (D)4个
 (10)如图,某建筑工地搭建的脚手架局部类似于4×2×3的长方体框架(由24个棱长为1个单位长度的正方体框架组合而成).一建筑工人从
(10)如图,某建筑工地搭建的脚手架局部类似于4×2×3的长方体框架(由24个棱长为1个单位长度的正方体框架组合而成).一建筑工人从
A点沿脚手架到点B,每步走1个单位长度,
且不连续向上攀登,则其行走的最近路线共
有 ( B )
(A)150条 (B)525条
(C)840条 (D)1260条
二、填空题:本大题共6小题,每小题5分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位置上.
(11)不等式 的解集为 ▲ .答案:
的解集为 ▲ .答案:
(12)函数 的最小正周期T= ▲ .答案:π
的最小正周期T= ▲ .答案:π
(13)过双曲线 的左焦点且垂直于x轴的直线与双曲线相交于M,N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于 ▲ .答案:2
的左焦点且垂直于x轴的直线与双曲线相交于M,N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于 ▲ .答案:2
(14)已知O是△ABC内一点, ,则△AOB与△AOC的面积的比值为 ▲ .
,则△AOB与△AOC的面积的比值为 ▲ .
答案:
(15)在 的二项展开式中,所有有理项之和为S,当x=2时,S等于 ▲ .答案:2048
的二项展开式中,所有有理项之和为S,当x=2时,S等于 ▲ .答案:2048
(16)已知集合A={(x,y)│|x|+|y|=2,x,y∈R},B={(x,y)│|xy|=a,x,y∈R},若A∩B中的元素所对应的点恰好是一个正八边形的八个顶点,则正数a的值为 ▲ .答案:
三、解答题:本大题共5小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(17)(本小题满分14分)
袋中装有20个不同的小球,其中有n( ,n>1)个红球,4个蓝球,10个黄球,其余为白球.已知从袋中取出3个颜色相同的彩球(不是白球)的概率为
,n>1)个红球,4个蓝球,10个黄球,其余为白球.已知从袋中取出3个颜色相同的彩球(不是白球)的概率为 .
.
(Ⅰ)求袋中的红球、白球各有多少个?
(Ⅱ)从袋中任取3个小球,求其中一定有红球的概率.
解:(Ⅰ)设“从袋中任取3球全为红球”、“从袋中任取3球全为蓝球”、“从袋中任取3 球全为黄球”分别为事件A,B,C,由题意知,A,B,C两两互斥,则
 ,
, . …………………………………………4分
. …………………………………………4分
故从袋中取出成3个都是相同颜色彩球(不是白球)的概率为
 =
= ,
,
∴ . …………………………………………………6分
. …………………………………………………6分
由此得从袋中取3球不可能全为红球,从而 .又
.又 ,n>1,故
,n>1,故 .
.
答:袋中有2个红球4个白球. …………………………………………………………8分
(Ⅱ)设“从袋中任取3个小球,其中一定有红球”为事件D,则
 =
= .
.
 答:从袋中任取3个小球,一定有红球的概率为
答:从袋中任取3个小球,一定有红球的概率为 .………………………………14分
.………………………………14分
(18)(本小题满分14分)
如图,在长方体 中,
中, ,
, ,
,
 ,M为AB的中点,E,F分别为
,M为AB的中点,E,F分别为 和AD1的中点.
和AD1的中点.
(Ⅰ)求证:直线EF⊥平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的大小.
所成角的大小.
解法一:(Ⅰ)延长AE交A1B1于点N,则点N为A1B1的中点.
连D1N,∵E,F分别是A
∴EF∥D1N.…………………………………………………………………………2分
在Rt△A ,
,
∴Rt△A
又AA1⊥D1N,A
(Ⅱ)过点A1作A1H⊥AN,垂足为H,连D1H.由三垂线定理,得 D1H⊥AN,
∴AN ⊥平面A1D1H,∴平面A1D1 H⊥平面AEF.
∴A1D1在平面AEF中的射影即为D1H,
∠A1D1H就是A1D1与平面AEF所成的角.………………………………………10分
在Rt△AA1N中,AA1=2,A1N= ,∴A1H=
,∴A1H= .
.
tan∠A1D1H= =
= ,故直线A1D1与平面AEF所成的角为arctan
,故直线A1D1与平面AEF所成的角为arctan .
.
∵AD∥A1D1,∴直线AD与平面AEF所成的角为arctan .…………………14分
.…………………14分
解法二:(Ⅰ)以A为原点,AB为x轴,AD为y轴,AA1为z轴建立空间坐标系.
则A(0,0,0),B( ,0,0),C(
,0,0),C( ,1,0),D(0,1,0),A1(0,0,2),
,1,0),D(0,1,0),A1(0,0,2),
B1( ,0,2),C1(
,0,2),C1( ,1,2),D(0,1,2).
,1,2),D(0,1,2).
∴ =(0,0,2),
=(0,0,2), =(
=( ,1,0).
,1,0).
又M( ,0,0),E(
,0,0),E( ,0,1),F(0,
,0,1),F(0, ,1),
,1),
∴ =(-
=(- ,
, ,0). ………………………………………………………3分
,0). ………………………………………………………3分
由 ?
? =(-
=(- ,
, ,0)?(0,0,2)=0,
,0)?(0,0,2)=0,
 ?
? =(-
=(- ,
, ,0)?(
,0)?( ,1,0)=0,∴
,1,0)=0,∴ ⊥
⊥ ,
, ⊥
⊥ .
.
又A
(Ⅱ)设向量n=(1,x,y)是平面AEF的一个法向量.
由(Ⅰ),可得 =(-
=(- ,0,1),
,0,1), =(0,
=(0, ,1). ………………8分
,1). ………………8分
由 ?n=0,
?n=0, ?n=0,得
?n=0,得 解之,得
解之,得
故n=(1, ,-
,- ). ……………………………………………………11分
). ……………………………………………………11分
设直线AD与平面AEF所成的角为α,则sinα= =
= =
= .
.
所以设直线AD与平面AEF所成的角为arcsin .…………………………14分
.…………………………14分
(19)(本小题满分14分)
将圆 按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使
按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使  =λa,求直线l的方程及对应的点C的坐标.
=λa,求直线l的方程及对应的点C的坐标.
解:圆 化为标准方程为
化为标准方程为 ,
,
按向量a=(-1,2)平移得⊙O方程为 x2+y2=5.……………………………………2分
∵ =λa,且|
=λa,且| |=|
|=| |,∴
|,∴ ⊥
⊥ ,
, ∥a. ……………………5分
∥a. ……………………5分
∴kAB= .设直线l的方程为y=
.设直线l的方程为y= x+m,联立,得
x+m,联立,得
将方程(1)代入(2),整理得5x2+4mx+
设A(x1,y1),B(x2,y2),则
x1+x2=- ,y1+y2=
,y1+y2= ,
, =(-
=(- ,
, ). ……………………………10分
). ……………………………10分
因为点C在圆上,所以 ,解之,得
,解之,得 .
.
此时,(※)式中的△=
所求的直线l的方程为2x-4y+5=0,对应的C点的坐标为(-1,2);或直线l的方程为2x-4y-5=0,对应的C点的坐标为(1,-2).……………………………………14分
解法二:同解法一,得⊙O的方程 .……………………………………………………2分
.……………………………………………………2分
由 =λa,有|
=λa,有| |=|λa |,从而λ=±1.……………………………………………5分
|=|λa |,从而λ=±1.……………………………………………5分
(1)当λ=1时, =a=(-1,2),所以C(-1,2).从而OC的中点为M(-
=a=(-1,2),所以C(-1,2).从而OC的中点为M(- ,1).
,1).
由 ,可得点M在AB上,又由
,可得点M在AB上,又由 ,
,
得直线的l的方程为 ,即
,即 .………………………………9分
.………………………………9分
(2)当λ=-1时, =-a=(1,-2),所以C(1,-2).
=-a=(1,-2),所以C(1,-2).
OC的中点为N( ,-1).
,-1).
同样由点N在AB上,可得直线l方程为 . ……………………………12分
. ……………………………12分
所求的直线l的方程为2x-4y+5=0,对应的C点的坐标为(-1,2);或直线l的方程为2x-4y-5=0,对应的C点的坐标为(1,-2).……………………………………14分
(20)(本小题满分14分)
已知 是定义在R上的函数,对于任意的实数a,b,都有
是定义在R上的函数,对于任意的实数a,b,都有 ,且
,且 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的解析式(
的解析式( ).
).
解:(Ⅰ)令 ,则
,则 ,从而
,从而 .……………………2分
.……………………2分
由 ,可得
,可得 .………………5分
.………………5分
(Ⅱ) .
.
设 ,则
,则 .…………………………………………………9分
.…………………………………………………9分
两边同乘以 ,可以得到
,可以得到 ,即
,即 .
.
故数列 为公差为
为公差为 等差数列. ……………………………………………12分
等差数列. ……………………………………………12分
由 ,可得
,可得 ,
,
所以 ,即
,即 . ……………………………………………14分
. ……………………………………………14分
(21)(本小题满分14分)
设函数 =x|x-a|+b.
=x|x-a|+b.
(Ⅰ)求证: 为奇函数的充要条件是a2+b2=0;
为奇函数的充要条件是a2+b2=0;
(Ⅱ)设常数b<2 -3,且对任意x∈[0,1],
-3,且对任意x∈[0,1], <0恒成立,求实数a的取值范围.
<0恒成立,求实数a的取值范围.
解:(Ⅰ)充分性:若a2+b2=0时,即a=b=0,所以 f(x)=x | x|.
∵f(-x)=-x |-x|=-x |x|=-f(x),对一切x∈R恒成立,
∴f(x)是奇函数. ……………………………………………………………………2分
必要性:若f(x)是奇函数,则对一切x∈R,f(-x)=-f(x)恒成立,即
-x |-x-a|+b=-x |x-a|-b.
令x=0,得b=-b,所以b=0.………………………………………………………4分
再令x=a,得
(Ⅱ)解法一:∵b<2 -3<0,∴当x=0时,a取任意实数不等式恒成立,
-3<0,∴当x=0时,a取任意实数不等式恒成立,
故考虑x∈(0,1]时,原不等式变为 | x-a |<- ,即 x+
,即 x+ <a<x-
<a<x- .
.
∴只需对x∈(0,1],满足 ………………………………8分
………………………………8分
对(1)式,由b<0时,在(0,1]上,f(x)=x+ 为增函数,
为增函数,
∴(x+ )max=f(1)=1+b.
)max=f(1)=1+b.
∴a>1+b. (3) ……………………………10分
对(2)式,当-1≤b<0时,在(0,1]上,x- =x+
=x+ ≥2
≥2 .
.
当x= 时,x-
时,x- =2
=2 ,∴(x-
,∴(x- )min=2
)min=2 .
.
∴a<2 .
(4)
.
(4)
由(3)、(4),要使a存在,必须有 即-1≤b<-3+2
即-1≤b<-3+2 .
.
∴当-1≤b<-3+2 时,1+b <a<2
时,1+b <a<2 .……………………………………12分
.……………………………………12分
当b<-1时,在(0,1]上,f(x)=x- 为减函数,(证明略)
为减函数,(证明略)
∴(x- )min=f(1)=1-b.
)min=f(1)=1-b.
∴当b<-1时,1+b <a<1-b.
综上所述,当-1≤b<2 -3时,a的取值范围是(1+b,2
-3时,a的取值范围是(1+b,2 );当b<-1时,a的取值范围是(1+b,1-b).………………………………………………………14分
);当b<-1时,a的取值范围是(1+b,1-b).………………………………………………………14分
解法二:f(x)=x|x-a|+b<0(x∈[0,1],b<2 -3恒成立,即x|x-a|<-b.
-3恒成立,即x|x-a|<-b.
由于b是负数,故x2-ax<-b,且x2-ax>b.
(1)x2-ax<-b在x∈[0,1],b<2 -3恒成立,设g(x)= x2-ax+b,
-3恒成立,设g(x)= x2-ax+b,
则 即
即
其中(1),(3)显然成立,由(2),得a>1+b.(※)………………………………8分
(2)x2-ax-b>0在x∈[0,1],b<2 -3恒成立,设h(x)= x2-ax-b,
-3恒成立,设h(x)= x2-ax-b,
① 即a<0.
即a<0.
结合(※),得b<-1时,1+b<a<0;-1≤b<2 -3时,a值不存在. ……9分
-3时,a值不存在. ……9分
② 即
即
结合(※),得b<-1时,0<a≤2;-1≤b<2 -3时,b+1<a<2
-3时,b+1<a<2 .…11分
.…11分
③ 即
即
结合(※),得b<-1时,2<a<1-b;-1≤b<2 -3时,a不存在.………12分
-3时,a不存在.………12分
综上,得-1≤b<2 -3时,b+1<a<2
-3时,b+1<a<2 ;b<-1时,b+1<a<1-b.…14分
;b<-1时,b+1<a<1-b.…14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com