
题目列表(包括答案和解析)
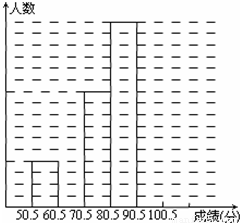
| 频率分布表 | ||
| 分组 | 频数 | 频率 |
| 50.5-60.5 | 4 | 0.08 |
| 60.5-70.5 | M | 0.16 |
| 70.5-80.5 | 10 | 0.20 |
| 80.5-90.5 | 16 | |
| 90.5-100.5 | n | |
| 合计 | 1 | |
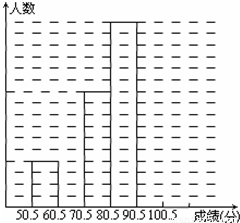
| 频率分布表 | ||
| 分组 | 频数 | 频率 |
| 50.5-60.5 | 4 | 0.08 |
| 60.5-70.5 | M | 0.16 |
| 70.5-80.5 | 10 | 0.20 |
| 80.5-90.5 | 16 | |
| 90.5-100.5 | n | |
| 合计 | 1 | |
通过对大学生手机消费情况的调查,探讨影响当代大学生购买手机决策的因素.研究者通过随机抽样对北师大、北大两地共150名被测试者进行了调查,其中男生占45.2%,女生占54.8%.请自愿的被测试者填写自制手机调查问卷(本问卷主要涵盖三方面内容:手机本身因素,服务及购买物理环境因素,广告及品牌效应因素.题目共16道,并随机排序,其中无关题1道).同时,研究人员还在区内各大手机专卖店收集相关资料.本研究一共发放问卷150份,有效回收率为90%.对问卷原始数据大致归类后,再对部分题目进行分析.
在手机本身特点上被测试者选择结果(见表一)
表一 被测试者对手机质量的选择
| 次数 | 百分比 | 有效百分 | 累积百分 | |
有效的 | 持久耐用 | 23 | 15.5 | 16.8 | 16.8 |
信号灵敏 | 54 | 36.5 | 39.4 | 56.2 | |
实用省电 | 12 | 8.1 | 8.8 | 65.0 | |
功能齐全 | 47 | 31.8 | 34.3 | 99.3 | |
其他 | 1 | 0.7 | 0.7 | 100.0 | |
总和 | 137 | 92.6 | 100.0 |
| |
遗漏值 | 系统界定的遗漏值 | 11 | 7.4 |
|
|
总和 |
| 148 | 100.0 |
|
|
在品牌、广告问题上被试关注(结果见表二)
表二 被测试者对广告中认为最可信的因素的选择结果
| 次数 | 百分比 | 有效百分 | 累积百分 | |
有效的 | 专业人士 | 43 | 29.1 | 29.5 | 29.5 |
名人 | 9 | 6.1 | 6.2 | 35.6 | |
统计数据 | 69 | 46.6 | 47.3 | 82.9 | |
其他 | 25 | 16.9 | 17.1 | 100.0 | |
总和 | 146 | 98.6 | 100.0 |
| |
遗漏值 | 系统界定的遗漏值 | 2 | 14 |
|
|
总和 |
| 148 | 100.0 |
|
|

被测试者对最有效的品牌公司形象塑造的策略的选择对以上所搜集的数据以表格或图表分类,在此研究基础上试表述对所搜集的数据处理的结果.并分析潜在因素对大学生购买决策的影响,试从心理特点加以阐释.
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
D
A
B
D
B
C
B
C
D
B
1.提示:
 ,故选C。
,故选C。
2.提示:“任意的”否定为“存在”;“>”的否定为“ ”,故选A
”,故选A
3.提示: 又
又 ,所以
,所以 ,故选D。
,故选D。
4.提示:在AB上取点D,使得 ,则点P只能在AD内运动,则
,则点P只能在AD内运动,则 ,
,
5.提示:排除法选B。
6.提示:由图(1)改为图(2)后每次循环时 的值都为1,因此运行过程出现无限循环,故选D
的值都为1,因此运行过程出现无限循环,故选D
7.提示:由茎叶图的定义,甲得分为7,8,9,15,19,23,24,26,32,41。共11个数,19是中位数,乙得分为5,7,11,11,13,20,22,30,31,40。共11个数,13是中位数。
故选B。
8.提示: 得
得 所以
所以 ,故选C。
,故选C。
 9.提示:由
9.提示:由 及
及 得
得
 如图
如图
过A作 于M,则
于M,则



 得
得 .
.
故选B.
10.提示:不妨设点(2,0)与曲线 上不同的三的点距离为分别
上不同的三的点距离为分别 ,它们组成的等比数列的公比为
,它们组成的等比数列的公比为 若令
若令 ,显然
,显然 ,又
,又 所以
所以 ,
, 不能取到
不能取到 。故选B。
。故选B。
11.提示:使用特值法:取集合 当
当 可以排除A、B;
可以排除A、B;
取集合 ,当
,当 可以排除C;故选D;
可以排除C;故选D;
12.提示:n棱柱有 个顶点,被平面截去一个三棱锥后,可以分以下6种情形(图1~6)
个顶点,被平面截去一个三棱锥后,可以分以下6种情形(图1~6)






2在图4,图6所示的情形,还剩 个顶点;
个顶点;
在图5的情形,还剩 个顶点;
个顶点;
在图2,图3的情形,还剩 个顶点;
个顶点;
在图1的情形,还剩下 个顶点.故选B.
个顶点.故选B.
二、填空题:
13.4
提示:
 由(1),(2)得
由(1),(2)得 或
或 ,所以
,所以 。
。
14.
提示:斜率 ,切点
,切点 ,所以切线方程为:
,所以切线方程为:
15.
提示:当 时,不等式无解,当
时,不等式无解,当 时,不等式变为
时,不等式变为 ,
,
由题意得 或
或 ,所以,
,所以, 或
或
16.
三、解答题:
17.解:① ∵ ∴
∴ 的定义域为R;
的定义域为R;
② ∵ ,
,
∴ 为偶函数;
为偶函数;
③ ∵ , ∴
, ∴ 是周期为
是周期为 的周期函数;
的周期函数;
④ 当 时,
时, =
= ,
,
∴当 时
时 单调递减;当
单调递减;当 时,
时,
 =
= ,
,
 单调递增;又∵
单调递增;又∵ 是周期为
是周期为 的偶函数,∴
的偶函数,∴ 在
在 上单调递增,在
上单调递增,在 上单调递减(
上单调递减( );
);
⑤ ∵当 时
时 ;
;
当 时
时 .∴
.∴ 的值域为
的值域为 ;
;
⑥由以上性质可得: 在
在 上的图象如图所示:
上的图象如图所示:

18.解:(Ⅰ)取PC的中点G,连结EG,GD,则
由(Ⅰ)知FD⊥平面PDC, 面PDC,所以FD⊥DG。
面PDC,所以FD⊥DG。
所以四边形FEGD为矩形,因为G为等腰Rt△RPD斜边PC的中点,
所以DG⊥PC,
|