题目列表(包括答案和解析)
如图，将一张矩形的纸对折以后略微展开，竖立在桌面上，说明折痕为什么与桌面垂直．
从图中可直观地看出，折痕垂直于对折后的纸与桌面所形成的交线．由直线与平面垂直的判定定理知，折痕与桌面垂直．那么在折痕垂直于纸与桌面的交线未知的情况下，单凭折后的纸与桌面垂直，能否得出折痕与桌面垂直？转化为数学语言，即如果两个相交平面都垂直于第三个平面，那么它们的交线也垂直于第三个平面吗？下面用不同的方法证明．
如图，已知平面α⊥平面β，平面α⊥平面γ，且β∩γ＝a，β∩α＝l，γ∩α＝m．
求证：a⊥α．
刘徽的割圆术以半径为单位长求圆内正六边形、十二边形等的每一边长，所得答数和2sinA(A是正多边形所对圆心角的一半)的值相符．以后公元十二世纪赵友钦用圆正四边形起算也同此理．利用他们的算法可以得出7.5°，15°，22.5°，30°，45°等角的正弦值的近似值．
此外，在古代的历法中有计算二十四个节气的日晷影长．地面上直立一个八尺长的“表”，太阳光对该“表”在地面上的射影由于地球公转而每个节气的影长都不同，这些影长和八尺长的“表”的比，构成一个余切函数表．
阅读上面材料，怎样利用刘徽的割圆术求7.5°，15°，22.5°，30°，45°等角的正弦值的近似值？
已知函数
．（
）
（1）若
在区间
上单调递增，求实数
的取值范围；
（2）若在区间
上，函数的图象恒在曲线
下方，求的取值范围．
【解析】第一问中，首先利用在区间上单调递增，则
在区间上恒成立，然后分离参数法得到
，进而得到范围；第二问中，在区间上，函数的图象恒在曲线下方等价于
在区间上恒成立．然后求解得到。
解：（1）在区间上单调递增，
则在区间上恒成立． …………3分
即，而当
时，
，故
．
…………5分
所以
．
…………6分
（2）令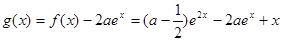
，定义域为
．
在区间上，函数的图象恒在曲线下方等价于在区间上恒成立．
∵
…………9分
① 若
，令
，得极值点
，
，
当
，即
时，在（
，+∞)上有
，此时
在区间
上是增函数，并且在该区间上有
，不合题意；
当
，即
时，同理可知，在区间上递增，
有
，也不合题意；
…………11分
② 若
，则有
，此时在区间上恒有
，从而在区间上是减函数；
要使在此区间上恒成立，只须满足
，
由此求得的范围是
． …………13分
综合①②可知，当
时，函数的图象恒在直线下方．
（08年聊城市一模） 给出以下命题：
①合情推理是由特殊到一般的推理，得到的结论不一定正确，演绎推是由一般到特殊的推理，得到的结论一定正确。
②甲、乙两同学各自独立地考察两个变量X、Y的线性相关关系时，发现两人对X的观察数据的平均值相等，都是s，对Y的观察数据的平均值也相等，都是t，各自求出的回归直线分别是l1、l2，则直线l1与l2必定相交于点（s，t）。
③某企业有职工150人，其中高级职称15人，中级职称45人，一般职员90人，若用分层抽样的方法抽出一个容量为30的样本，则一般职员应抽出20人。
④用独立性检验（2×2列联表法）来考察两个分类变量是否有关系时，算出的随机变量K2的值越大，说明“X与Y有关系”成立的可能性越大。
其中真命题的序号是 （写出所有真命题的序号）。
在棱长为
的正方体
中,
是线段
的中点,
.
(1) 求证:
^
；
(2) 求证://平面
；
(3) 求三棱锥
的表面积.
【解析】本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中，利用
，得到结论，第二问中，先判定
为平行四边形，然后
，可知结论成立。
第三问中，
是边长为
的正三角形，其面积为
，
因为
平面
，所以
，
所以
是直角三角形，其面积为
，
同理
的面积为
，
面积为
. 所以三棱锥的表面积为
.
解: (1)证明：根据正方体的性质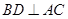
，
因为
，
所以
，又
，所以，
，
所以^.
………………4分
(2)证明：连接
，因为
，
所以为平行四边形，因此
，
由于是线段的中点，所以， …………6分
因为
面，
平面，所以∥平面. ……………8分
(3)是边长为的正三角形，其面积为，
因为平面，所以，
所以是直角三角形，其面积为，
同理的面积为，
……………………10分
面积为. 所以三棱锥的表面积为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com