
题目列表(包括答案和解析)
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
|
|
视觉记忆能力 |
||||
|
偏低 |
中等 |
偏高 |
超常 |
||
|
听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
|
中等 |
1 |
8 |
3 |
|
|
|
偏高 |
2 |
|
0 |
1 |
|
|
超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为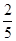 .
.
(I)试确定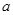 、
、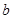 的值;
的值;
(II)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(III)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为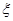 ,求随机变量
,求随机变量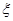 的数学期望
的数学期望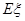 .
.
【解析】1)中由表格数据可知,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的学生共有(10+a)人.记“视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上”为事件A,则P(A)=(10+a)/40=2/5,解得a=6.……………2分
所以.b=40-(32+a)=40-38=2答:a的值为6,b的值为2.………………3分
(2)中由表格数据可知,具有听觉记忆能力或视觉记忆能力超常的学生共有8人.
方法1:记“至少有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件B,
则“没有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件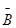
(3)中由于从40位学生中任意抽取3位的结果数为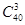 ,其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共24人,从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的结果数为
,其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共24人,从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的结果数为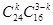 ,………………………7分
,………………………7分
所以从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的概率为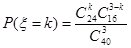 ,k=0,1,2,3
,k=0,1,2,3
| 6 |
| A、A=30°,B=45° | ||
B、c=1,cosC=
| ||
| C、B=60°,c=3 | ||
| D、C=75°,A=45° |
袋子中装有大小形状完全相同的m个红球和n个白球,其中m,n满足m>n≥2且m+n≤l0(m,n∈N+),若从中取出2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.
(Ⅰ) 求m,n的值;
(Ⅱ) 从袋子中任取3个球,设取到红球的个数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
【解析】第一问中利用 ,解得m=6,n=3.
,解得m=6,n=3.
第二问中, 的取值为0,1,2,3. P(
的取值为0,1,2,3. P( =0)=
=0)= 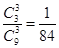 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
得到分布列和期望值
解:(I)据题意得到 解得m=6,n=3.
解得m=6,n=3.
(II) 的取值为0,1,2,3.
的取值为0,1,2,3.
P( =0)=
=0)= 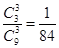 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
 的分布列为
的分布列为

所以E =2
=2
已知函数 。
。
(1)求函数的最小正周期和最大值;
(2)求函数的增区间;
(3)函数的图象可以由函数 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
【解析】本试题考查了三角函数的图像与性质的运用。第一问中,利用 可知函数的周期为
可知函数的周期为 ,最大值为
,最大值为 。
。
第二问中,函数 的单调区间与函数
的单调区间与函数 的单调区间相同。故当
的单调区间相同。故当 ,解得x的范围即为所求的区间。
,解得x的范围即为所求的区间。
第三问中,利用图像将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的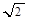 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
解:(1)函数 的最小正周期为
的最小正周期为 ,最大值为
,最大值为 。
。
(2)函数 的单调区间与函数
的单调区间与函数 的单调区间相同。
的单调区间相同。
 即
即
 所求的增区间为
所求的增区间为 ,
,
 即
即
 所求的减区间为
所求的减区间为 ,
, 。
。
(3)将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的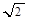 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
| 6 |
| A.A=30°,B=45° | B.c=1,cosC=
| ||
| C.B=60°,c=3 | D.C=75°,A=45° |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com