
题目列表(包括答案和解析)
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
已知函数 .
.
(I)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当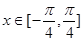 时,函数
时,函数 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
三.解答题(解答应写出文字说明,证明过程或演算步骤):
17. (本小题满分12分)
已知等比数列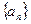 中,
中,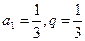 ,
,
(1)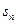 为数列
为数列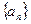 前
前 项的和,证明:
项的和,证明:
(2)设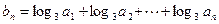 ,求数列
,求数列 的通项公式;
的通项公式;
(17) (本小题满分12分)在△ABC中,BC=2![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求AB的值;w.w.(Ⅱ)求![]() 的值.
的值.
17(本小题满分12分)
设等差数列![]() 满足
满足![]() ,
,![]() 。
。
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)求![]() 的前
的前![]() 项和
项和![]() 及使得
及使得![]() 最大的序号
最大的序号![]() 的值。
的值。
((本小题满分12分)
编号分别为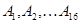 的16名篮球运动员在某次比赛中得分记录如下;
的16名篮球运动员在某次比赛中得分记录如下;
|
编号 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
|
得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
|
编号 |
A9 |
A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
|
得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
(Ⅰ)将得分在对应区间的人数填入相应的空格内:
|
区 间 |
|
|
|
|
人 数 |
|
|
|
(Ⅱ)从得分在区间 内的运动员中随机抽取2人.
内的运动员中随机抽取2人.
(1)用运动员编号列出所有可能的抽取结果;
(2)求这两人得分之和大于50的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com