
题目列表(包括答案和解析)
对于给定数列
{cn},如果存在实常数p,q使得cn+1=pcn+q对于任意n∈N+都成立,我们称数列{cn}是“M类数列”.(1)若an=2n,bn=3·2n,n∈N+,数列{an},{bn}是否为“M类数列”?若是,指出它对应的实常数p,q;若不是,请说明理由;
(2)求证:若数列{an}是“M类数列”,则数列{an+an+1}也是“M类数列”.
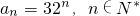 ,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由;
,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由;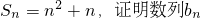 是“M类数列”.
是“M类数列”.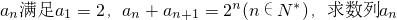 前2013项的和.
前2013项的和. ,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由;
,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由; 是“M类数列”.
是“M类数列”. 前2013项的和.
前2013项的和. ,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由;
,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由; 是“M类数列”.
是“M类数列”. 前2013项的和.
前2013项的和.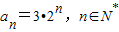 ,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由;
,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由;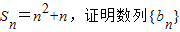 是“M类数列”.
是“M类数列”.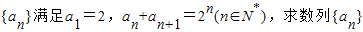 前2013项的和.
前2013项的和.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com