
题目列表(包括答案和解析)
|
若数列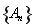 满足
满足 ,则称数列
,则称数列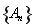 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列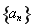 中,
中,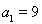 ,点
,点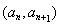 在函数
在函数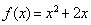 的图象上,其中
的图象上,其中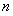 为正整数.
为正整数.
(1)证明数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列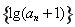 为等比数列;
为等比数列;
(2)设(1)中“平方递推数列”的前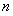 项积为
项积为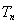 ,
,
即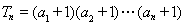 ,求
,求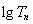 ;
;
(3)在(2)的条件下,记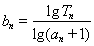 ,求数列
,求数列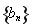 的前
的前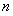 项和
项和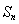 ,并求使
,并求使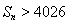 的
的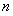 的最小值.
的最小值.
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为ξ.
(1)求ξ的分布列;
(2)求1件产品的平均利润(即ξ的);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com