练习册

  • 练习册
  • 试题
    由此得: 【查看更多】

     

    题目列表(包括答案和解析)

    由原点O向三次曲线y=x3-3ax2（a≠0）引切线，切点为P1（x1，y1）（O，P1两点不重合），再由P1引此曲线的切线，切于点P2（x2，y2）（P1，P2不重合），如此继续下去，得到点列：{Pn（xn，yn）}
    （1）求x1；
    （2）求xn与xn+1满足的关系式；
    （3）若a＞0，试判断xn与a的大小关系，并说明理由

    查看答案和解析>>

    由原点O向三次曲线y=x3-3ax2+bx（a≠0）引切线，切于不同于点O的点P1（x1，y1），再由P1引此曲线的切线，切于不同于P1的点P2（x2，y2），如此继续地作下去，…，得到点列{Pn（xn，yn）}，试回答下列问题：
    （1）求x1；
    （2）求xn与xn+1的关系；
    （3）若a＞0，求证：当n为正偶数时，xn＜a；当n为正奇数时，xn＞a．

    查看答案和解析>>

    由坐标原点O向曲线y=x3-3ax2+bx（a≠0）引切线，切于O以外的点P1（x1，y1），再由P1引此曲线的切线，切于P1以外的点P2（x2，y2），如此进行下去，得到点列{ Pn（xn，yn}}．
    求：（Ⅰ）xn与xn-1（n≥2）的关系式；
    （Ⅱ）数列{xn}的通项公式．

    查看答案和解析>>

    由原点向三次曲线引切线,切于不同于点的点

    ，再由引此曲线的切线，切于不同于的点，如此继续地作下去,……,得到点列，试回答下列问题： ⑴求； (2)求与的关系式；

    (3)若，求证:当为正偶数时, ；当为正奇数时, .

    查看答案和解析>>

    由于当前学生课业负担较重，造成青少年视力普遍下降，现从某中学随机抽取16名学生，经校医用对数视力表检査得到每个学生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶)如下：

    (I )若视力测试结果不低于5 0，则称为“好视力”，求校医从这16人中随机选取3人，至多有1人是“好视力”的概率；

    (II)以这16人的样本数据来估计整个学校的总体数据，若从该校(人数很多）任选3人，记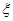表示抽到“好视力”学生的人数，求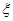的分布列及数学期望，据此估计该校高中学生（共有5600人）好视力的人数

     

    查看答案和解析>>


    同步练习册答案