
题目列表(包括答案和解析)
已知数列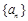 满足
满足 .
.
(1)求数列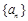 的通项公式;
的通项公式;
(2)对任意给定的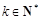 ,是否存在
,是否存在 (
(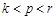 )使
)使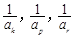 成等差数列?若存
成等差数列?若存
在,用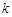 分别表示
分别表示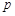 和
和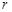 (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;
(3)证明:存在无穷多个三边成等比数列且互不相似的三角形,其边长为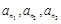 .
.
已知数列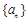 满足
满足 .
.
(1)证明数列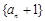 为等比数列,并求出数列
为等比数列,并求出数列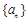 的通项公式;
的通项公式;
(2)若数列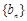 满足
满足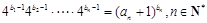 .证明:数列
.证明:数列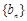 是等差数列.
是等差数列.
(3)证明: .
.
已知数列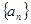 满足
满足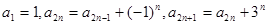 (
( ).
).
(1)求 的值;
的值;
(2)求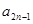 (用含
(用含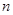 的式子表示);
的式子表示);
(3)记 ,数列
,数列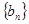
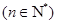 的前
的前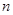 项和为
项和为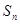 ,求
,求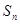 (用含
(用含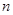 的式子表示).).
的式子表示).).
已知数列 满足
满足 (
( ).
).
(1)求 的值;
的值;
(2)求 (用含
(用含 的式子表示);
的式子表示);
(3)(理)记数列 的前
的前 项和为
项和为 ,求
,求 (用含
(用含 的式子表示).
的式子表示).
 满足
满足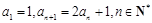 .
. 为等比数列,并求出数列
为等比数列,并求出数列 的通项公式;
的通项公式; 满足
满足 .证明:数列
.证明:数列 是等差数列.
是等差数列. .
.一、选择题:本大题共10小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
B
D
A
B
B
C
D
二、填空题:本大题7小题,每小题4分,共28分.
11、 ; 12、
; 12、  ; 13、
; 13、 ; 14、
; 14、 ; 15、
; 15、 ; 16、
; 16、 ;17、
;17、 或
或 。
。
三、解答题
18、(1)略 …………………………………………………………………………(7分)
(2) …………………………………………………………(14分)
…………………………………………………………(14分)
19、(1) tanA=
tanA=
 …………………(7分)
…………………(7分)
(2) 原式=
=  ……………………………………………………………………(14分)
……………………………………………………………………(14分)
20、(1)略 ……………………………………………………………………(7分)
(2) 就是二面角
就是二面角 的平面角,即
的平面角,即 ,
,
 …………………………………………………………………(9分)
…………………………………………………………………(9分)
取 中点
中点 ,则
,则 平面
平面 ,
,
 就是
就是 与平面
与平面 所成的角。 …………………………(11分)
所成的角。 …………………………(11分)
 ,
, ,
,
所以 与平面
与平面 所成的角的大小为
所成的角的大小为 。 …………………………(14分)
。 …………………………(14分)
(用向量方法,相应给分)
21、(1) ,
,
又 在区间(-∞,0)及(4,+∞)上都是增函数,在区间(0,4)上是减函数,
在区间(-∞,0)及(4,+∞)上都是增函数,在区间(0,4)上是减函数, 又
又 .………(6分)
.………(6分)
(2)
当点 是切点时,切线方程为9x+6y-16=0.………………(10分)
是切点时,切线方程为9x+6y-16=0.………………(10分)
当点 不是切点时,切点为
不是切点时,切点为 ,
,
得 所以切点为
所以切点为 ,
,
切线方程为 .……………………………………(14分)
.……………………………………(14分)
22、解:解:(1)、设 ,则
,则 ,
,
∵点P分 所成的比为
所成的比为 ∴
∴  ∴
∴ 
∴ 代入
代入 中,得
中,得 为P点的轨迹方程.
为P点的轨迹方程.
当 时,轨迹是圆. …………………………………………………(8分)
时,轨迹是圆. …………………………………………………(8分)
(2)、由题设知直线l的方程为 , 设
, 设
联立方程组 ,消去
,消去 得:
得:
∵ 方程组有两解 ∴  且
且 ∴
∴ 或
或 且
且
∵
 ∴
∴
又 ∵
 ∴
∴  解得
解得 (舍去)或
(舍去)或
∴ 曲线C的方程是 ……………………………………………(16分)
……………………………………………(16分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com