练习册

  • 练习册
  • 试题
    18． 甲.乙两位小学生各有2008年奥运吉祥物“福娃 5个(其中“贝贝 .“晶晶 .“欢欢 . 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分12分）
    甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个（其中“贝贝”、“晶晶”、“欢欢”、
    “迎迎”和“妮妮各一个”），现以投掷一个骰子的方式进行游戏，规则如下：当出现向上的点数是奇数时，甲赢得乙一个福娃；否则乙赢得甲一个福娃，规定掷骰子的次数达9次时，或在此前某人已赢得所有福娃时游戏终止．记游戏终止时投掷骰子的次数为
    （1）求掷骰子的次数为7的概率；
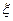
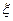    （2）求的分布列及数学期望E．

    查看答案和解析>>

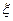    （本小题满分12分）

    甲、乙两位学生参加数学竞赛培训，现分别从他们的培训期间参加的若干次预赛成中随机抽取8次，记录如下

    甲：82，91，79，78，95，88，83，84

    乙：92，95，80，75，83，80，90，85

    （I）        画出甲、乙两位学生成绩的茎叶图；

    （II）      现要从中选派一人参加数学竞赛，从统计学角度，你认为派哪位学生参加合请说明理由。

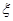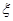    （III）     若将频率视为概率，对学生甲在今后的三次数学竞赛成绩进行预测，记这三次成绩中高于80分的次数为，求的分布列及数学期望E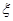

     

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    （本小题满分12分）

            甲、乙两位学生参加数学建模竞赛培训，现分别从他们在培训期间参加的若干次预

    赛成绩中随机抽取8次，记录如下：

        甲：72  71  69  68  85  78  83  74

        乙：82  85  70  65  73  70  80  75

       （Ⅰ）画出甲、乙两位学生成绩的茎叶图，指出学生乙成绩的中位数；

       （Ⅱ）现要从中选派一人参加数学建模竞赛，从平均状况和方差的角度考虑，你认为派哪位学生参加合适?请说明理由；

       （Ⅲ）若将频率视为概率，对学生甲在今后的三次数学建模竞赛成绩进行预测，记这三次成绩中高于80分的次数为ξ，求ξ的分布列及数学期望Eξ．

     

     

    查看答案和解析>>

    （本小题满分12分）

    甲、乙两位学生参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，记录如下：

                    甲：82  81  79  78  95  88  93  84

                    乙：92  95  80  75  83  80  90  85

    （1）用茎叶图表示这两组数据，并写出乙组数据的中位数；

    （2）经过计算知甲、乙两人预赛的平均成绩分别为，甲的方差为，现要从中选派一人参加数学竞赛，你认为选派哪位学生参加较合适？请说明理由；

    （3）现规定80分以上为合格成绩，90分以上为优秀成绩，从甲的合格成绩中随机抽出2个，则抽出优秀成绩的概率有多大？

     

     

     

     

     

     

    查看答案和解析>>

    （本小题满分12分）

      甲、乙两位篮球运动员进行定点投蓝，每人各投4个球，甲投篮命中的概率为，乙投篮命中的概率为．

     (1)求甲至多命中2个且乙至少命中2个的概率；

     (2)若规定每投篮一次命中得3分，未命中得分，求乙所得分数的概率分布和数学期望．

    查看答案和解析>>

     

    一、选择题：本大题共12小题，每小题5分，共60分。

    CABD  CDDC  BABD

    二、填空题：本大题共4小题，每小题4分，共16分。

    13．3                             14．1200                15．          16．

    三、解答题：本大题共6小题，共74分。

    17．解：                                                                               1分

           ∵，∴⊥，∴∠

           在Rt△ADC中                                                         4分

           ∴                                                                                                         6分

           ∵                                               7分

           又∵                      9分

           ∴

                                                                                  12分

    18．解：（1）当=7时，甲赢意味着“第七次甲赢，前6次赢5次，但根据规则，前5次中必输1次”，由规则，每次甲赢或乙赢的概率均为，因此

           =                                                            4分

       （2）设游戏终止时骰子向上的点数是奇数出现的次数为，向上的点数是偶数出现的次数为n，则由，可得：当

           或，时，当，或因此的可能取值是5、7、9                                                                             6分

           每次投掷甲赢得乙一个福娃与乙赢得甲一个福娃的可能性相同，其概率都是

                   10分

           所以的分布列是：

    5

    7

    9

                                                                        12分

    19．解：设数列的公比为

       （1）若，则

           显然不成等差数列，与题设条件矛盾，所以≠1                            1分

           由成等差数列，得

           化简得                                           4分

           ∴                                                                              5分

       （2）解法1：                                      6分

           当≥2时，

                                                                                                                                  10分

          

          

          

           =1+                                                              12分

           解法2：                                              6分

           当≥2时，设这里，为待定常数。

           则

           当n≥2时，易知数列为单调递增数列，所以

           可见，n≥2时，

           于是，n≥2时，有                                         10分

          

          

           =1+                                                                          12分

    20．解法一：如图建立空间直角坐标系，

       （1）有条件知                                                1分

           由面⊥面ABC，AA1⊥A1C，AA1=A1C，知              2分

          

           ∵                                ……………3分

           ∴与不垂直，即AA1与BC不垂直，

           ∴AA1与平面A1BC不垂直……5分

       （2）由ACC1A1为平行四边形，

           知==…7分

           设平面BB1C1C的法向量，

           由

           令，则                                       9分

           另外，平面ABC的法向量（0，0，1）                                                  10分

          

           所以侧面BB1C1C与底面ABC所成锐二面角的余弦值为                                12分

           解法二：（1）取AC中点D，连结A1D，则A1D⊥AC。

           又∵侧面ACC1A1与底面ABC垂直，交线为AC，

           ∵A1D⊥面ABC                                      ………2分

           ∴A1D⊥BC。

           假设AA1与平面A1BC垂直，则A1D⊥BC。

           又A1D⊥BC，由线面垂直的判定定理，

           BC⊥面A1AC，所以BC⊥AC，这样在△ABC中

           有两个直角，与三角形内角和定理矛盾。假设不

           成立，所以AA1不与平面A1BC垂直………5分

       （2）侧面BB1C1C与底面ABC所成的锐二面角即为侧面BB1C1C与A1B1C1底面所成的锐二面角。

           过点C作A1C1的垂线CE于E，则CE⊥面A1B1C1，B1C1⊥CE。

           过点E作B1C1的垂线EF于F，连结CF。

           因为B1C1⊥EF，B1C1⊥CE，所以B1C1⊥面EFC，B1C1⊥CF

           所以∠CFE即为所求侧面BB1C1C与地面A1B1C1所成的锐二面角的平面角     9分

           由得

           在Rt△ABC中，cos∠

           所以，侧面BB1C1C与底面ABC所成锐二面角的余弦值为                     12分

    21．（1）设与在公共点处的切线相同。

           。由题意知

           即                                                                      2分

           解得或（舍去，）                       4分

          

           可见                                                                               7分

       （2）

           要使在（0，4）上单调，

           须在（0，4）上恒成立    8分

           在（0，4）上恒成立在（0，4）上恒成立。

           而且可为足够小的正数，必有                        9分

           在（0，4）上恒成立

           或                                                                                                     11分

           综上，所求的取值范围为，或，或                           12分

    22．（1）∵点A的坐标为（）

           ∴，椭圆方程为    ①…1分

           又∵，且BC过椭圆M的中心

           （0，0），∴                 ……2分

           又∵∴△AOC是以∠C为直角的等腰三角形，

           易得C点坐标为（，）               ……3分

           将（，）代入①式得

           ∴椭圆M的方程为              ……4分

       （2）当直线的斜率，直线的方程为

           则满足题意的t的取值范围为……5分

           当直线的斜率≠0时，设直线的方程为

          

           由得                                      6分

           ∵直线与椭圆M交于两点P、Q，

           ∴△=

           即                                      ②                                                     8分

           设P（x1，y1），Q（x2，y2），PQ中点，则

           *的横坐标，纵坐标，

           D点的坐标为（0，-2）

           由，得⊥，，

           即即。   ③                                                     11分

           ∴∴。                                                               ④

           由②③得，结合④得到                                                      13分

           综上所述，                                                                                    14分

     

     

     

     

     

     


    同步练习册答案