为了解高中一年级学生身高情况，某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查，测得身高频数分布表如下表1、表2．

表1：男生身高频数分布表

 

身高（cm）	[160，165）	[165，170）	[170，175）	[175，180）	[180，185）	[185，190）
频数	2	5	14	13	4	2

 

表2：女生身高频数分布表

 

身高（cm）	[150，155）	[155，160）	[160，165）	[165，170）	[170，175）	[175，180）
频数	1	7	12	6	3	1

 

（I）求该校男生的人数并完成下面频率分布直方图；

（II）估计该校学生身高在的概率；

（III）从样本中身高在180190cm之间的男生中任选2人，求至少有1人身高在185190cm之间的概率。

【解析】第一问样本中男生人数为40 ，

由分层抽样比例为10%可得全校男生人数为400

（2）中由表1、表2知，样本中身高在的学生人数为：5+14+13+6+3+1=42，样本容量为70 ，所以样本中学生身高在的频率 

故由估计该校学生身高在的概率 

（3）中样本中身高在180185cm之间的男生有4人，设其编号为①②③④ 样本中身高在185190cm之间的男生有2人，设其编号为⑤⑥从上述6人中任取2人的树状图，故从样本中身高在180190cm之间的男生中任选2人得所有可能结果数为15，求至少有1人身高在185190cm之间的可能结果数为9，因此，所求概率

由表1、表2知，样本中身高在的学生人数为：5+14+13+6+3+1=42，样本容量为70 ，所以样本中学生身高在

的频率-----------------------------------------6分

故由估计该校学生身高在的概率．--------------------8分

（3）样本中身高在180185cm之间的男生有4人，设其编号为①②③④ 样本中身高在185190cm之间的男生有2人，设其编号为⑤⑥从上述6人中任取2人的树状图为：

--10分

故从样本中身高在180190cm之间的男生中任选2人得所有可能结果数为15，求至少有1人身高在185190cm之间的可能结果数为9，因此，所求概率

 

在四棱锥中，平面，底面为矩形，.

（Ⅰ）当时，求证：；

（Ⅱ）若边上有且只有一个点，使得，求此时二面角的余弦值.

【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时，底面ABCD为正方形，

又因为,………………2分

又，得证。

第二问，建立空间直角坐标系，则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分

设BQ=m，则Q(1，m,0)(0《m《a》

要使，只要

所以，即………6分

由此可知时，存在点Q使得

当且仅当m=a-m，即m=a/2时，BC边上有且只有一个点Q，使得

由此知道a=2,  设平面POQ的法向量为

,所以    平面PAD的法向量

则的大小与二面角A-PD-Q的大小相等所以

因此二面角A-PD-Q的余弦值为

解：(Ⅰ)当时，底面ABCD为正方形，

又因为,又………………3分

(Ⅱ) 因为AB,AD,AP两两垂直，分别以它们所在直线为X轴、Y轴、Z轴建立坐标系，如图所示，

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分

设BQ=m，则Q(1，m,0)(0《m《a》要使，只要

所以，即………6分

由此可知时，存在点Q使得

当且仅当m=a-m，即m=a/2时，BC边上有且只有一个点Q，使得由此知道a=2,

设平面POQ的法向量为

,所以    平面PAD的法向量

则的大小与二面角A-PD-Q的大小相等所以

因此二面角A-PD-Q的余弦值为

 

解：因为有负根，所以在y轴左侧有交点，因此

解：因为函数没有零点，所以方程无根，则函数y=x+|x-c|与y=2没有交点，由图可知c>2

 13．证明：（1）令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0

若f(1)=0，f(0)=f(1×0)=f(1)f(0)=0，所以f(1)=f(0)与已知条件“”矛盾所以f(1)≠0，因此f(1)=1,所以f(1)-1=0，1是函数y=f(x)-1的零点

（2）因为f(1)=f[(-1)×（-1）]=f2(-1)=,所以f(-1)=±1，但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1，只能等于-1。所以任x∈R，f(-x)=f(-1)f(x)=-f(x)，因此函数是奇函数

数字1，2，3，4恰好排成一排，如果数字i（i=1，2，3，4）恰好出现在第i个位置上则称有一个巧合，求巧合数的分布列。

在棱长为的正方体中,是线段的中点,.

(1) 求证:^；

(2) 求证://平面；

(3) 求三棱锥的表面积.

【解析】本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中，利用，得到结论，第二问中，先判定为平行四边形，然后，可知结论成立。

第三问中，是边长为的正三角形，其面积为，

因为平面，所以，

所以是直角三角形，其面积为，

同理的面积为， 面积为.  所以三棱锥的表面积为.

解: (1)证明：根据正方体的性质，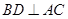

因为，

所以，又，所以，，

所以^.               ………………4分

(2)证明：连接，因为，

所以为平行四边形，因此，

由于是线段的中点，所以，      …………6分

因为面，平面，所以∥平面.   ……………8分

(3)是边长为的正三角形，其面积为，

因为平面，所以，

所以是直角三角形，其面积为，

同理的面积为，              ……………………10分

面积为.          所以三棱锥的表面积为

 

解：能否投中，那得看抛物线与篮圈所在直线是否有交点。因为函数的零点是-2与4，篮圈所在直线x=5在4的右边，抛物线又是开口向下的，所以投不中。

某城市出租汽车的起步价为10元，行驶路程不超出4km，则按10元的标准收租车费若行驶路程超出4km，则按每超出lkm加收2元计费(超出不足1km的部分按lkm计)．从这个城市的民航机场到某宾馆的路程为15km．某司机常驾车在机场与此宾馆之间接送旅客，由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定，每停车5分钟按lkm路程计费)，这个司机一次接送旅客的行车路程ξ是一个随机变量，

（１）他收旅客的租车费η是否也是一个随机变量？如果是，找出租车费η与行车路程ξ的关系式；

(２)已知某旅客实付租车费38元，而出租汽车实际行驶了15km，问出租车在途中因故停车累计最多几分钟?这种情况下，停车累计时间是否也是一个随机变量？