
题目列表(包括答案和解析)
设椭圆 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 在椭圆上且异于
在椭圆上且异于 两点,
两点, 为坐标原点.
为坐标原点.
(Ⅰ)若直线 与
与 的斜率之积为
的斜率之积为 ,求椭圆的离心率;
,求椭圆的离心率;
(Ⅱ)若 ,证明直线
,证明直线 的斜率
的斜率
 满足
满足
【解析】(1)解:设点P的坐标为 .由题意,有
.由题意,有 ①
①
由 ,得
,得 ,
,
由 ,可得
,可得 ,代入①并整理得
,代入①并整理得
由于 ,故
,故 .于是
.于是 ,所以椭圆的离心率
,所以椭圆的离心率
(2)证明:(方法一)
依题意,直线OP的方程为 ,设点P的坐标为
,设点P的坐标为 .
.
由条件得 消去
消去 并整理得
并整理得 ②
②
由 ,
, 及
及 ,
,
得 .
.
整理得 .而
.而 ,于是
,于是 ,代入②,
,代入②,
整理得
由 ,故
,故 ,因此
,因此 .
.
所以 .
.
(方法二)
依题意,直线OP的方程为 ,设点P的坐标为
,设点P的坐标为 .
.
由P在椭圆上,有
因为 ,
, ,所以
,所以 ,即
,即 ③
③
由 ,
, ,得
,得 整理得
整理得 .
.
于是 ,代入③,
,代入③,
整理得
解得 ,
,
所以 .
.
甲船由 岛出发向北偏东
岛出发向北偏东 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为 海里∕小时,在甲船从
海里∕小时,在甲船从 岛出发的同时,乙船从
岛出发的同时,乙船从 岛正南
岛正南 海里处的
海里处的 岛出发,朝北偏东
岛出发,朝北偏东 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为 海里∕小时。
海里∕小时。
⑴求出发 小时时两船相距多少海里?
小时时两船相距多少海里?
⑴ 两船出发后多长时间相距最近?最近距离为多少海里?
【解析】第一问中根据时间得到出发 小时时两船相距的海里为
小时时两船相距的海里为

第二问设时间为t,则
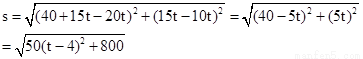
利用二次函数求得最值,
解:⑴依题意有:两船相距

答:出发3小时时两船相距 海里
海里

⑵两船出发后t小时时相距最近,即

即当t=4时两船最近,最近距离为 海里。
海里。
已知数列 是公差不为零的等差数列,
是公差不为零的等差数列,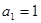 ,且
,且 、
、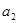 、
、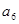 成等比数列。
成等比数列。
⑴求数列 的通项公式;
的通项公式;
⑵设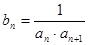 ,求数列
,求数列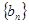 的前
的前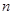 项和
项和 。
。
【解析】第一问中利用等差数列 的首项为
的首项为 ,公差为d,则依题意有:
,公差为d,则依题意有:
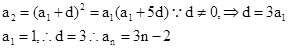
第二问中,利用第一问的结论得到数列的通项公式,
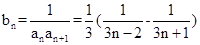 ,利用裂项求和的思想解决即可。
,利用裂项求和的思想解决即可。
| 1 |
| 2 |
| ∫ | n 0 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com