
题目列表(包括答案和解析)
(理)(本小题满分12分)
口袋里装有大小相同的4个红球和8个白球,甲、乙两人依规则从袋中有放回摸球,每次摸出一个球,规则如下:若一方摸出一个红球,则此人继续下一次摸球;若一方摸出一个白球,则由对方接替下一次摸球,且每次摸球彼此相互独立,并由甲进行第一次摸球;求在前三次摸球中,甲摸得红球的次数ξ的分布列及数学期望.
(理)(本小题满分12分)已知y=f(x)是偶函数,当x>0时, ,
,
且当 时,
时, 恒成立,求
恒成立,求 的最小值.
的最小值.
(理)(本小题满分12分)
直四棱柱 中,底面
中,底面 为菱形,且
为菱形,且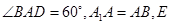 为
为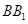 延长线上的一点,
延长线上的一点, 面
面 .
.
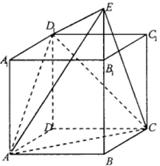
(Ⅰ)求二面角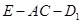 的大小;
的大小;
(Ⅱ)在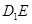 上是否存在一点
上是否存在一点 ,使
,使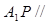 面
面 ?若存在,求
?若存在,求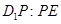 的值;不存在,说明理由.
的值;不存在,说明理由.
(理)(本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2 000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡).某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中是省外游客,其余是省内游客.在省外游客中有持金卡,在省内游客中有持银卡.
(1)在该团中随机采访2名游客,求恰有1人持银卡的概率;
(2)在该团中随机采访2名游客,求其中持金卡与持银卡人数相等的概率
(理)(本小题满分12分)已知y=f(x)是偶函数,当x>0时,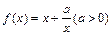 ,
,
且当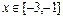 时,
时,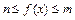 恒成立,求
恒成立,求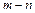 的最小值.
的最小值.
第1卷
一、选择题
1.D 2.B 3.B 4.C 5.A 6.C.files/image104.gif) 7.B 8.A 9.D 10.C 11.A 12.A
7.B 8.A 9.D 10.C 11.A 12.A
第Ⅱ卷
二、填空题
13..files/image002.gif)
14.(理).files/image107.gif) (文)3x+3y-2=0
(文)3x+3y-2=0
15.(-3,0).files/image109.gif) (3,+∞)
(3,+∞)
16.②④
三、解答题
17.(Ⅰ)这批食品不能出厂的概率是:
.files/image111.gif)
(Ⅱ)五项指标全部检验完毕,这批食品可以出厂的概率是:
.files/image113.gif)
五项指标全部检验完毕,这批食品不能出厂的概率是:
.files/image115.gif)
由互斥事件有一个发生的概率加法公式可知,五项指标全部检验完毕,
才能确定这批食品出厂与否的概率是:
.files/image117.gif)
18.(Ⅰ)设f(x)=ax+b(a≠0),则c的方程为:
.files/image119.gif) ①
①
由点(2,.files/image121.gif) )在曲线c上,得1=
)在曲线c上,得1=.files/image123.gif) (2一b).
②
(2一b).
②
由①②解得a=b=1,∴曲线c的方程为y=x-1.
(Ⅱ)由,点(n+1,.files/image125.gif) )底曲线c上,有
)底曲线c上,有.files/image125.gif) =n
=n
于是.files/image127.gif) .
..files/image129.gif) ?…?
?…?.files/image131.gif) ,
,
即.files/image133.gif)
注意到a1=1,所以an=(n-1)!
(Ⅲ).files/image135.gif)
.files/image137.gif)
.files/image139.gif)
.files/image141.gif)
.files/image143.gif)
∴.files/image145.gif) .
.
19.(甲)(Ⅰ)选取DA1、DC、DD1,分别为Ox、Oy、Oy轴建立空间直角坐标,易知E(0,0,.files/image036.gif) ),F(
),F(.files/image036.gif) ,
,.files/image036.gif) ,0),B1(1,1,1),C(0,1,0),
,0),B1(1,1,1),C(0,1,0),
.files/image148.gif) ,
,
.files/image150.gif)
=0,
.files/image152.gif) .
.
(Ⅱ)G(0,.files/image154.gif) ,-1),Cl(0,1,1),
,-1),Cl(0,1,1),
.files/image156.gif)
.files/image158.gif) .
.
(Ⅲ).files/image160.gif) ,
,
.files/image162.gif)
.files/image164.gif)
.files/image166.gif)
(乙)
(Ⅰ)用反证法易证B1D1与A1D不垂直.
(Ⅱ)由余弦有cos∠AC1D1=.files/image168.gif)
设AC1=x,则.files/image170.gif)
.files/image172.gif) 上
上
单调递增.
.files/image174.gif)
(Ⅲ)∵A1B1∥C1D1,∴∠AC1D1为异面直线AC1与A1B1所成角.
由余弦定理,有.files/image176.gif)
设AC1=x,则.files/image178.gif)
.files/image180.gif)
.files/image182.gif)
故AC1与A1B1所成角的取值范围是.files/image184.gif)
20.(理)解:
(Ⅰ)∵f(x)与g(x)的图像关于直线x-1=0对称,
∴f(x)=g(2-x).
.files/image186.gif) ,
,
f(x)=g(2一x)=-ax+2x3.
又f(x)是偶函数,∴.files/image188.gif)
f(x)=f(-x)=ax一2x3.
.files/image190.gif)
(Ⅱ)f(x)=a-6x2,∵f(x)为[0,1]上的增函数.
∴f'(x)=a-6x2≥0,
∴a≥6x2在.files/image192.gif) 上,恒成立.
上,恒成立.
∵x.files/image194.gif) [0,1)时,6x2≤6,∴a≥6.
[0,1)时,6x2≤6,∴a≥6.
即a的取值范围是[6,+∞).
(Ⅲ)当a在[0,1)上的情形.
由f'(x)=0,得.files/image196.gif) 得a=6.此时x=1
得a=6.此时x=1
∴当a.files/image194.gif) (-6,6)时,f(x)的最大值不可能是4.
(-6,6)时,f(x)的最大值不可能是4.
(文)
(1).files/image198.gif)
(2)根据题意可得.files/image200.gif) ,
,
整理得(ax-a)(ax+a-1)<0.
由于a>1,所以x<1.
.files/image202.gif)
.files/image204.gif)
即.files/image206.gif) .
.
21.解:
(Ⅰ)∵|PF1|一|PF2|=2a,又|PF1|=3|PF2|.
∴|PF1|=3a,|PF2|=a.
设F1(-c,0),F2(c,0),P(x0,y0),由.files/image208.gif) 得3a=ex0+a,则x0=
得3a=ex0+a,则x0=.files/image210.gif) .
.
∵P在双曲线右支上,∴x1≥a,即.files/image210.gif) ≥a,解得
≥a,解得
1<e≤2.
∴e的最大值为2,此时.files/image212.gif)
∴渐近线方程为.files/image214.gif) ,
,
(Ⅱ).files/image216.gif) .
.
又.files/image218.gif) .
.
∴.files/image220.gif) .
.
又.files/image222.gif) .
.
.files/image224.gif) .
.
∴b2=C2-a2=6.
∴双曲线方程为.files/image226.gif) .
.
22.(理)解:
(1)可求得f(x)=.files/image228.gif) .
.
由f(x)<f(1)得.files/image200.gif) .
.
整理得(ax-a)(ax+a―1)<0.
由于a>l,所以x<1.
(Ⅱ).files/image231.gif)
=.files/image233.gif) ,
,
由.files/image235.gif) ,
,
.files/image237.gif) ,
,
即f(2)>2f(1).
.files/image239.gif)
即f(3)>3f(1).
(Ⅲ)更一般地,有:f(n)>nf(1) (n.files/image194.gif)
.files/image241.gif) *,n≥2).
*,n≥2).
用数学归纳法证明,
①由(Ⅱ)知n=2,3时,不等式成立.
②假设n=k时,不等式成立,即f(k)>kf(1).
.files/image243.gif)
.files/image245.gif)
.files/image247.gif)
.files/image249.gif) .
.
这说明n=k+1时,不等式也成立.
由①②可知,对于一切.files/image251.gif) ,均有f(x)>nf(1).
,均有f(x)>nf(1).
(文)解:
(Ⅰ)∵f(x)与g(x)的图像关于直线x-1=0对称.
∴f(x)=g(2-x),当x.files/image194.gif) [-1,0]时,2一x
[-1,0]时,2一x.files/image194.gif) [2,3]
[2,3]
f(x)=g(2一x)=一ax+2x3.
又∵f(x)是偶函数,∴x.files/image194.gif) [0,1]时,一x
[0,1]时,一x.files/image194.gif) [一1,0]
[一1,0]
f(x)=f(一x)=ax一2x3.
.files/image253.gif)
(Ⅱ).files/image255.gif) 上的增函数.
上的增函数.
.files/image257.gif) 上恒成立
上恒成立
.files/image259.gif) .
.
即a的取值范围是[6,+∞].
(Ⅲ)只考虑在[0,1)上的情形.
由.files/image261.gif) .
.
∴当.files/image263.gif) 的最大值不可能是4.
的最大值不可能是4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com