
题目列表(包括答案和解析)
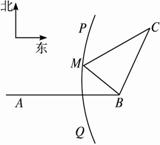
(04年福建卷理)如图,B地在A地的正东方向4 km处,C地在B地的北偏东30º方向2 km处,河流的没岸PQ(曲线)上任意一点到A的距离比到B的距离远2 km。现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物。经测算,从M到B、M两地修建公路的费用分别是a万元/km、2a万元/km,那么修建这两条公路的总费用最低是
(A)(2![]() -2)a万元 (B)5a万元
-2)a万元 (B)5a万元
(C)(2![]() +1)a万元 (D)(2
+1)a万元 (D)(2![]() +3)a万元
+3)a万元

| 2 |
A.(![]() +1)a万元
+1)a万元
B.(![]() -2)a万元
-2)a万元
C.![]() a万元
a万元
D.( ![]() -1)a万元
-1)a万元

现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.
(1)经测算,从M到B、C两地修建公路的费用都是a万元/千米,那么修建这两条公路的总费用最低是( )
A. (![]() +1)a万元
+1)a万元
B. (2![]() -2)a万元
-2)a万元
C.2![]() a万元
a万元
D. (![]() -1)a万元
-1)a万元
(2)经测算,从M到B、M到C修建公路的费用分别为a万元/千米、2a万元/千米,那么修建这两条公路的总费用最低是( )
A. (2![]() -2)a万元
-2)a万元
B.5a万元
C. (2![]() +1)a万元
+1)a万元
D. (2![]() +3)a万元
+3)a万元
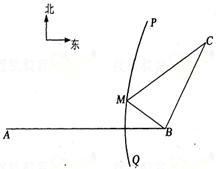
如图,B地在A地的正东方向4 km处,C地在B地的北
偏东30°方向2 km处,河流的沿岸PQ(曲线)上任意一点
到A的距离比到B的距离远2 km..现要在曲线PQ上选一处
M建一座码头,向B、C两地转运货物.那么这两条公路MB、
MC的路程之和最短是 km
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com