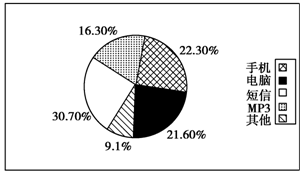
科学技术在青少年中的影响日益扩大。某学校对学生们使用现代化产品，包括电脑上网，发送短信，听MP3等进行了一次调查，结果如下图。请根据图中的信息，写一篇英语短文，并针对这些信息发表你的看法，词数120~150。

?

V. 书面表达
假定你是李华，David 是你的美国笔友。他对中国鼓励使用环保购物袋很感兴趣，来信向你询问此事。请你给他写封回信。主要内容如下：感谢他的关注, 简要介绍相关情况并谈谈你的感想。
注意：
1.   词数100左右，信的格式已为你写好。
2.   可根据内容要点适当增加细节，以使行文连贯。
3. 参考词汇：环抱购物袋---environment-friendly shopping bag; 关注---concern.
_______________________________________________________________________________  _______________________________________________________________________________  _______________________________________________________________________________                                         

假定你是李华，David 是你的美国笔友。 他对中国鼓励使用环保购物袋很感兴趣，来信询问此事。 请你给他写封回信，主要内容如下：

# 感谢他的关注      

# 简要介绍相关情况

# 谈谈你的感想

注意：1 字数100左右，信的格式已为你写好。

2 可根据内容要点适当增加细节，以使行文连贯。

3 参考词汇   环保购物袋 ---- environmental-friendly shopping bag

关注 ---- concern

                                                             June 8

Dear David,

_________________________________________________________________________________

_________________________________________________________________________________

_____________________________________________________

 Yours, Li Hua

根据下面的汉语提示写一篇英语短文，词数120左右。

某中学新建的电子阅览室即将投入使用，一次能容纳200名学生。学校正征询学生意见。假如你是其中的一名学生，请根据以下要点对阅览室的使用提出建议，并陈述理由：

1．电子阅览室的开放时间

2．向学生提供的浏览项目

3．安全管理等注意事项

—————————————————————————————————————————————

—————————————————————————————————————————————

—————————————————————————————————————————————

—————————————————————————————————————————————

—————————————————————————————————————————————

书面表达（满分25分）
假定你是李华，David 是你的美国笔友。他对中国鼓励使用环保购物袋很感兴趣，来信向你询问此事。请你给他写封回信。主要内容如下：
感谢他的关注。
简要介绍相关情况。
谈谈你的感想。
注意：
词数100左右，信的格式已为你写好。
可根据内容要点适当增加细节，以使行文连贯。