练习册

  • 练习册
  • 试题
    6．函数的最小正周期是 ．学科网 【查看更多】

     

    题目列表(包括答案和解析)

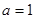    “”是“函数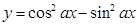”的最小正周期为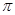”的（      ）

    A．充分不必要条件           B．必要不充分条件

    C．充要条件                 D．既不充分也不必要条件[来源:学.科.网]

     

    查看答案和解析>>

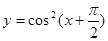    函数是

    A．最小正周期是π的偶函数B．最小正周期是π的奇函数学科网
    C．最小正周期是2π的偶函数D．最小正周期是2π的奇函数学科网

    查看答案和解析>>

    已知函数，给出下列四个命题：

    ①若

    ②的最小正周期是；

    ③在区间上是增函数；[来源:学科网]

    ④的图象关于直线对称；

    ⑤当时，的值域为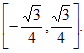

    其中正确的命题为                            （    ）

           A．①②④     B．③④⑤     C．②③       D．③④

    查看答案和解析>>

    已知函数，给出下列四个命题：学科网

         ①若，则；   ②的最小正周期是；学科网

         ③在区间上是增函数；  ④的图象关于直线对称学科网

         A．①②④     B．①③     C．②③     D．③④学科网

    查看答案和解析>>

    下列命题正确的是(    )[来源:学科网ZXXK]

        A．函数在区间内单调递增

        B．函数的最小正周期为

        C．函数的图像是关于点成中心对称的图形

        D．函数的图像是关于直线成轴对称的图形

    查看答案和解析>>

    一、填空题

    1．   2．,    3．    4．2   5．1     6．

    7．50   8．  9．-2   10．    11．2     12．

    13．2     14．

    二、解答题

    15[解]：证：设   ,连 。                    

     ⑴  ∵为菱形，   ∴ 为中点，又为中点。

          ∴∥                              （5分） 

          又 , ∴∥（7分）

     ⑵ ∵为菱形，   ∴,              （9分）

       又∵，  ∴   （12分）

       又     ∴ 又

             ∴             （14分）

    16[解]：解：⑴ ∵ ， ∴  ，∴ （1分）

           又                         （3分）

            ∴

            ∴ 。                        （6分）

            ⑵， （8分）

            ∵，∴， 。

            ∴                （10分）

             

                 （13分）

              （当 即 时取“”）   

    所以的最大值为,相应的    (14分)

    17．解：⑴直线的斜率 ，中点坐标为 ，

            ∴直线方程为     （4分）

            ⑵设圆心，则由在上得：

                                 ①      

            又直径,,

    又         

    ∴            ②       （7分）

    由①②解得或

    ∴圆心 或                  

    ∴圆的方程为  或  （9分）                         

     ⑶  ，∴ 当△面积为时 ，点到直线的距离为 。                   （12分）

     又圆心到直线的距离为，圆的半径 且    

    ∴圆上共有两个点使 △的面积为  .  （14分）

    18[解] (1)乙方的实际年利润为：  ．   (5分)

    ，

    当时，取得最大值．

    　　    所以乙方取得最大年利润的年产量 (吨)．…………………8分

    　(2)设甲方净收入为元，则．

    学科网(Zxxk.Com)　将代入上式，得：．   (13分)

    　　　　又

    　　　　令，得．

    　　　　当时，；当时，，所以时，取得最大值．

    　　　　因此甲方向乙方要求赔付价格 (元／吨)时，获最大净收入．　 (16分)

     

    19. 解：⑴ 由 得 ，令 得  （2分）

       ∴所求距离的最小值即为到直线的距离（4分）

                          （7分）

       ⑵假设存在正数，令 则（9分）

       由得：  

       ∵当时， ，∴为减函数；

       当时，，∴ 为增函数.

       ∴         （14分）

    ∴   ∴

    ∴的取值范围为        （16分）

     

    20. 解：⑴由条件得：  ∴  （3分）

         ∵ ∴ ∴为等比数列∴（6分）

          ⑵由   得            （8分）

         又   ∴                    （9分）

     ⑶∵

              

    （或由即）

    ∴为递增数列。                              （11分）

    ∴从而       （14分）

    ∴

                                （16分）

    附加题答案

    21.         (8分)

    22. 解：⑴①当时，

           ∴                                                      （2分）

            ②当时，

           ∴                                                 （4分）

            ③当时，

           ∴                                                （6分）

           综上该不等式解集为                                   (8分)

    23. （1）；       (6分)

    （2）AB=              (12分)

    24. 解： ⑴设为轨迹上任一点，则

                                                 （4分）

           化简得：   为求。                                （6分）

           ⑵设，，

             ∵  ∴                        （8分）

             ∴ 或 为求                                   （12分）


    同步练习册答案