
题目列表(包括答案和解析)
(本题满分16分)
对于数列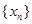 ,如果存在一个正整数
,如果存在一个正整数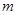 ,使得对任意的
,使得对任意的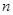 (
(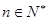 )都有
)都有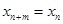 成立,那么就把这样一类数列
成立,那么就把这样一类数列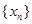 称作周期为
称作周期为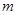 的周期数列,
的周期数列,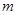 的最小值称作数列
的最小值称作数列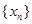 的最小正周期,以下简称周期.例如当
的最小正周期,以下简称周期.例如当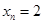 时
时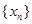 是周期为
是周期为 的周期数列,当
的周期数列,当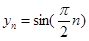 时
时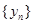 是周期为
是周期为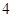 的周期数列.
的周期数列.
(1)设数列 满足
满足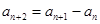 (
(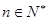 ),
),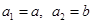 (
(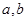 不同时为0),求证:数列
不同时为0),求证:数列 是周期为
是周期为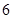 的周期数列,并求数列
的周期数列,并求数列 的前2012项的和
的前2012项的和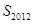 ;
;
(2)设数列 的前
的前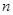 项和为
项和为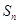 ,且
,且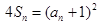 .
.
①若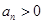 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
②若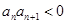 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
(3)设数列 满足
满足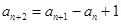 (
(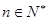 ),
),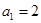 ,
,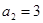 ,数列
,数列 的前
的前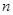 项和为
项和为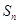 ,试问是否存在实数
,试问是否存在实数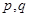 ,使对任意的
,使对任意的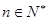 都有
都有 成立,若存在,求出
成立,若存在,求出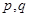 的取值范围;不存在,说明理由.
的取值范围;不存在,说明理由.
(本题满分16分)
设数列![]() 的通项是关于x的不等式
的通项是关于x的不等式![]()
![]() 的解集中整数的个
的解集中整数的个
数。(1)求![]() 并且证明
并且证明![]() 是等差数列;
是等差数列;
(2)设m、k、p∈N*,m+p=2k,求证:![]() +
+![]() ≥
≥![]() ;
;
(3)对于(2)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,
请证明你的结论,如果不成立,请说明理由.
(本题满分12分)
对于数列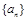 ,定义
,定义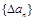 为数列
为数列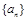 的一阶差分数列,其中
的一阶差分数列,其中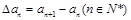 .
.
(Ⅰ)若数列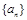 的通项公式
的通项公式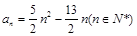 ,求
,求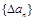 的通项公式;
的通项公式;
(Ⅱ)若数列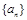 的首项是1,且
的首项是1,且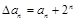 .
.
①设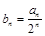
 ,求数列
,求数列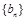 的通项公式;
的通项公式;
②求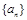 的前
的前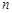 项和
项和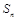 .
.
(本题满分16分)
设数列 满足
满足 ,令
,令 .
.
⑴试判断数列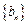 是否为等差数列?并说明理由;
是否为等差数列?并说明理由;
⑵若 ,求
,求 前
前 项的和
项的和 ;
;
⑶是否存在 使得
使得 三数成等比数列?
三数成等比数列?
(本题满分16分)
设数列 满足
满足 ,令
,令 .
.
⑴试判断数列 是否为等差数列?并说明理由;
是否为等差数列?并说明理由;
⑵若 ,求
,求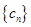 前
前 项的和
项的和 ;
;
⑶是否存在 使得
使得 三数成等比数列?
三数成等比数列?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com