
题目列表(包括答案和解析)
| a1+2a2+3a3+…+nan |
| 1+2+3+…+n |
| n(n+1)(2n+1) |
| 6 |
(本题满分16分)
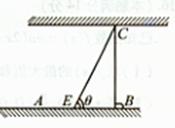
如图为河岸一段的示意图,一游泳者站在河岸的A点处,欲前往河对岸的C点处。若河宽BC为100m,A、B相距100m,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C。已知此人步行速度为v,游泳速度为0.5v。
(I)设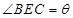 ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为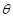 的函数;并求自变量
的函数;并求自变量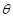 取值范围;
取值范围;
II)当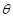 为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
(本题满分16分)设![]() ,
,![]()
(1)令![]() ,讨论
,讨论![]() 在(0.+∞)内的单调性并求极值;
在(0.+∞)内的单调性并求极值;
(2)求证:当![]() 时,恒有
时,恒有![]() 。
。
(本小题满分16分)已知三条直线 ,
,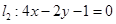 和
和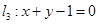 ,
,
(1)若此三条直线不能构成三角形,求实数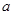 的取值范围;
的取值范围;
(2)已知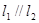 ,能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到
,能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到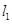 的距离是P点到
的距离是P点到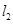 的距离的
的距离的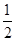 ;③P点到
;③P点到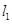 的距离与P点到
的距离与P点到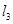 的距离之比是
的距离之比是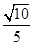 。若能,试求P点坐标;若不能,请说明理由。
。若能,试求P点坐标;若不能,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com