
题目列表(包括答案和解析)
在极坐标系中,圆 :
: 和直线
和直线 相交于
相交于 、
、 两点,求线段
两点,求线段 的长
的长
【解析】本试题主要考查了极坐标系与参数方程的运用。先将圆的极坐标方程圆 :
: 即
即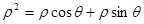 化为直角坐标方程即
化为直角坐标方程即 
然后利用直线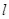
 即
即 ,得到圆心到直线的距离
,得到圆心到直线的距离 ,从而利用勾股定理求解弦长AB。
,从而利用勾股定理求解弦长AB。
解:分别将圆 和直线
和直线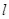 的极坐标方程化为直角坐标方程:
的极坐标方程化为直角坐标方程:
圆 :
: 即
即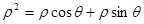 即
即  ,
,
即 , ∴ 圆心
, ∴ 圆心 ,
, ---------3分
---------3分
直线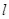
 即
即 , ------6分
, ------6分
则圆心 到直线
到直线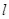 的距离
的距离 ,----------8分
,----------8分
则 即所求弦长为
即所求弦长为
在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为
 点
点 是曲线
是曲线 上的动点.
上的动点.
(1)求线段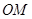 的中点
的中点 的轨迹的直角坐标方程;
的轨迹的直角坐标方程;
(2) 以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,若直线
轴的正半轴为极轴建立极坐标系,若直线 的极坐标方程为
的极坐标方程为 ,求点
,求点 到直线
到直线 距离的最大值.
距离的最大值.
【解析】第一问利用设曲线 上动点
上动点 ,由中点坐标公式可得
,由中点坐标公式可得
 所以点
所以点 的轨迹的参数方程为
的轨迹的参数方程为
 消参可得
消参可得
第二问,由题可知直线 的直角坐标方程为
的直角坐标方程为 ,因为原点到直线的距离为
,因为原点到直线的距离为 ,
,
所以点 到直线的最大距离为
到直线的最大距离为
在平面直角坐标系xoy中,已知曲线C1:x2+y2=1,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(2cosθ-sinθ)=6.
(Ⅰ)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的 、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.
、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.
(Ⅱ)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值.
【解析】(Ⅰ)根据极坐标与普通方程的互化,将直线l:ρ(2cosθ-sinθ)=6化为普通方程,C2的方程为 ,化为普通方程;(Ⅱ)利用点到直线的距离公式表示出距离,求最值.
,化为普通方程;(Ⅱ)利用点到直线的距离公式表示出距离,求最值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com