
题目列表(包括答案和解析)
设常数![]() ,函数
,函数![]() ,
,![]() .
.
(Ⅰ)令![]() ,求
,求![]() 的最小值,并比较
的最小值,并比较![]() 的最小值与零的大小;
的最小值与零的大小;
(Ⅱ)求证:![]() 在
在![]() 上是增函数;
上是增函数;
(Ⅲ)求证:当![]() 时,恒有
时,恒有![]() .
.
设常数a≥0,函数![]()
(1)令![]() ,求g(x)的最小值,并比较g(x)的最小值与零的大小;
,求g(x)的最小值,并比较g(x)的最小值与零的大小;
(2)求证:![]() 上是增函数;
上是增函数;
(3)求证:当![]()
已知数列{an}的前n项和 ,且
,且 的最大值为4.
的最大值为4.
(1)确定常数k的值,并求数列{an}的通项公式an;
(2)令 ,数列{bn}的前n项和为Tn,试比较Tn与
,数列{bn}的前n项和为Tn,试比较Tn与 的大小.
的大小.
已知数列{an}的前n项和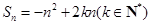 ,且
,且 的最大值为4.
的最大值为4.
(1)确定常数k的值,并求数列{an}的通项公式an;
(2)令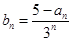 ,数列{bn}的前n项和为Tn,试比较Tn与
,数列{bn}的前n项和为Tn,试比较Tn与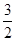 的大小.
的大小.
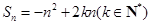 ,且
,且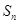 的最大值为4.
的最大值为4.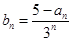 ,数列{bn}的前n项和为Tn,试比较Tn与
,数列{bn}的前n项和为Tn,试比较Tn与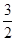 的大小.
的大小.一、填空题:本大题共14小题,每小题5分,计70分.
1.第二象限 2. 3
3.Π 4. /江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image170.gif) 5. _
5. _/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image172.gif) _ 6. 2
_ 6. 2/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image174.gif) 7.
7.
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image176.gif)
8. /江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image178.gif) 9. 10 10.向右平移
9. 10 10.向右平移/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image180.gif) 11. 3.5 12.①④
13.
11. 3.5 12.①④
13. /江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image182.gif) 14.①③
14.①③
二、解答题:本大题共6小题,计90分.
15.解:(1)/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image184.gif)
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image186.gif) .
.
又/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image188.gif) ,
,/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image190.gif) ,即
,即/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image192.gif) ,
,
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image194.gif) .
.
(2)/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image196.gif) ,
,/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image083.gif) ,
,
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image199.gif) 且
且/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image201.gif) ,
,
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image203.gif) ,即
,即/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image205.gif) 的取值范围是
的取值范围是/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image207.gif) .
.
16.(Ⅰ)证明:连结AF,在矩形ABCD中,因为AD=4,AB=2,点F是BC的中点,所以∠AFB=∠DFC=45°.所以∠AFD=90°,即AF⊥FD.又PA⊥平面ABCD,所以PA⊥FD.
所以FD⊥平面PAF. 故PF⊥FD.
(Ⅱ)过E作EH//FD交AD于H,则EH//平面PFD,且 AH=/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image209.gif) AD. 再过H作HG//PD交PA于G,则GH//平面PFD,且 AG=
AD. 再过H作HG//PD交PA于G,则GH//平面PFD,且 AG=/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image209.gif) PA. 所以平面EHG//平面PFD,则EG//平面PFD,从而点G满足AG=
PA. 所以平面EHG//平面PFD,则EG//平面PFD,从而点G满足AG=/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image209.gif) PA.
PA.
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image210.gif) 17.解:(1)由于⊙M与∠BOA的两边均相切,故M到OA及OB的距离均为⊙M的半
17.解:(1)由于⊙M与∠BOA的两边均相切,故M到OA及OB的距离均为⊙M的半
径,则M在∠BOA的平分线上,
同理,N也在∠BOA的平分线上,即O,M,N
三点共线,且OMN为∠BOA的平分线,
∵M的坐标为/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image212.gif) ,∴M到
,∴M到/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image099.gif) 轴的距离为1,即
轴的距离为1,即
⊙M的半径为1,
则⊙M的方程为/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image215.gif) ,
,
设⊙N的半径为/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image217.gif) ,其与
,其与/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image099.gif) 轴的的切点为C,连接MA、MC,
轴的的切点为C,连接MA、MC,
由Rt△OAM∽Rt△OCN可知,OM:ON=MA:NC,即/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image219.gif) ,
,
则OC=/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image221.gif) ,则⊙N的方程为
,则⊙N的方程为/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image223.gif) ;
;
(2)由对称性可知,所求的弦长等于过A点直线MN的平行线被⊙/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image106.gif) 截得的弦
截得的弦
的长度,此弦的方程是/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image225.gif) ,即:
,即:/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image227.gif) ,
,
圆心N到该直线的距离d=/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image229.gif) ,则弦长=
,则弦长=/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image231.gif) .
.
另解:求得B(/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image233.gif) ),再得过B与MN平行的直线方程
),再得过B与MN平行的直线方程/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image235.gif) ,圆心N到该直线的距离
,圆心N到该直线的距离/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image237.gif) =
=/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image229.gif) ,则弦长=
,则弦长=/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image231.gif) .
.
(也可以直接求A点或B点到直线MN的距离,进而求得弦长)
18.解(1)由题意/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image239.gif) 的中垂线方程分别为
的中垂线方程分别为/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image241.gif) ,
,
于是圆心坐标为/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image243.gif) …………………………………4分
…………………………………4分
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image131.gif) =
=/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image245.gif)
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image247.gif) >
>/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image133.gif) ,即
,即 /江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image249.gif) >
>/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image133.gif) 即
即/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image251.gif) >
>/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image133.gif) 所以
所以/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image253.gif) >
>/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image255.gif) ,
,
于是/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image257.gif) >
>/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image259.gif) 即
即/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image261.gif) >
>/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image263.gif) ,所以
,所以/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image265.gif) <
</江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image267.gif) 即
即 /江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image133.gif) <
</江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image270.gif) <
</江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image272.gif) ………………8分
………………8分
(2)假设相切, 则/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image274.gif) ,……………………………………………………10分
,……………………………………………………10分
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image276.gif) ,………13分
,………13分/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image278.gif) 这与
这与/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image133.gif) <
</江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image255.gif) <
</江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image281.gif) 矛盾.
矛盾.
故直线/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image135.gif) 不能与圆
不能与圆/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image126.gif) 相切. ………………………………………………16分
相切. ………………………………………………16分
19.解(Ⅰ)∵/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image285.gif) ,
,/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image287.gif)
∴/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image289.gif)
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image291.gif)
∴/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image293.gif) ,
,/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image287.gif) ∴
∴/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image295.gif) ,令
,令/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image297.gif) ,得
,得/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image299.gif) ,列表如下:
,列表如下:
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image099.gif)
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image302.gif)
2
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image304.gif)
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image306.gif)
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image308.gif)
0
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image310.gif)
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image147.gif)
递减
极小值/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image313.gif)
递增
∴/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image147.gif) 在
在/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image299.gif) 处取得极小值
处取得极小值/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image317.gif) ,
,
即/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image147.gif) 的最小值为
的最小值为/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image317.gif) .
.
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image319.gif) ,∵
,∵/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image321.gif) ,∴
,∴/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image323.gif) ,又
,又/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image137.gif) ,∴
,∴/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image326.gif) .
.
(Ⅱ)证明由(Ⅰ)知,/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image147.gif) 的最小值是正数,∴对一切
的最小值是正数,∴对一切/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image287.gif) ,恒有
,恒有/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image329.gif) 从而当
从而当/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image331.gif) 时,恒有
时,恒有/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image333.gif) ,故
,故/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image149.gif) 在
在/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image336.gif) 上是增函数.
上是增函数.
(Ⅲ)证明由(Ⅱ)知:/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image149.gif) 在
在/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image336.gif) 上是增函数,
上是增函数,
∴当/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image153.gif) 时,
时,/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image339.gif) , 又
, 又/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image341.gif) ,
,
∴/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image343.gif) ,即
,即/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image345.gif) ,∴
,∴/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image155.gif)
故当/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image153.gif) 时,恒有
时,恒有/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image155.gif) .
.
20.解:(1)数列{an}的前n项和/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image349.gif) ,
,
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image351.gif) …2分
…2分
又/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image353.gif) ,
,/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image355.gif) …………4分
…………4分
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image357.gif) 是正项等比数列,
是正项等比数列,/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image359.gif) , …………6分
, …………6分
公比/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image361.gif) ,数列
,数列/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image363.gif) …………8分
…………8分
(2)解法一:/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image365.gif) ,
,
由/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image367.gif) …………11分
…………11分
/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image369.gif) ,当
,当/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image371.gif) , …………13分
, …………13分
又/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image373.gif) 故存在正整数M,使得对一切
故存在正整数M,使得对一切/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image375.gif) M的最小值为2.…16分
M的最小值为2.…16分
(2)解法二:/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image377.gif) 令
令/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image379.gif) ,11分
,11分
由/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image381.gif) ,
,
函数/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image383.gif) ……13分
……13分
对于/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image385.gif)
故存在正整数M,使得对一切/江苏连云港外国语学校2008―2009学年度高三阶段性测试数学试卷2008.12.files/image387.gif) 恒成立,M的最小值为2.……16分
恒成立,M的最小值为2.……16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com