
题目列表(包括答案和解析)
(本小题满分14分)
已知函数![]() ,在定义域内有且只有一个零点,存在
,在定义域内有且只有一个零点,存在![]() , 使得不等式
, 使得不等式![]() 成立. 若
成立. 若![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(I)求数列![]() 的通项公式;
的通项公式;
(II)设各项均不为零的数列![]() 中,所有满足
中,所有满足![]() 的正整数
的正整数![]() 的个数称为这个数列
的个数称为这个数列![]() 的变号数,令
的变号数,令![]() (n为正整数),求数列
(n为正整数),求数列![]() 的变号数;
的变号数;
(Ⅲ)设![]() (
(![]() 且
且![]() ),使不等式
),使不等式
![]() 恒成立,求正整数
恒成立,求正整数![]() 的最大值.
的最大值.
(本小题满分12分)
(理)已知Sn是正数数列{an}的前n项和,S12,S22、……、Sn2 ……,是以3为首项,以1为公差的等差数列;数列{bn}为无穷等比数列,其前四项之和为120,第二项与第四项之和为90.
(I)求an、bn;(II)从数列{![]() }中能否挑出唯一的无穷等比数列,使它的各项和等于
}中能否挑出唯一的无穷等比数列,使它的各项和等于![]() .若能的话,请写出这个数列的第一项和公比?若不能的话,请说明理由.
.若能的话,请写出这个数列的第一项和公比?若不能的话,请说明理由.
(本小题满分13分)已知函数f (x)=2n![]() 在[0,+
在[0,+![]() 上最小值是a
上最小值是a![]() (n∈N*).
(n∈N*).
(1)求数列{a![]() }的通项公式;(2)已知数列{b
}的通项公式;(2)已知数列{b![]() }中,对任意n∈N*都有b
}中,对任意n∈N*都有b![]() a
a![]() =1成立,设S
=1成立,设S![]() 为数列{b
为数列{b![]() }的前n项和,证明:2S
}的前n项和,证明:2S![]() <1;(3)在点列A
<1;(3)在点列A![]() (2n,a
(2n,a![]() )中是否存在两点A
)中是否存在两点A![]() ,A
,A![]() (i,j∈N*),使直线A
(i,j∈N*),使直线A![]() A
A![]() 的斜率为1?若存在,求出所有的数对(i,j);若不存在,请说明理由.
的斜率为1?若存在,求出所有的数对(i,j);若不存在,请说明理由.
(本小题满分12分)
已知数列 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数 构成等差数列
构成等差数列 ,
, 是
是 的前n项和,且
的前n项和,且

( I )若数阵中从第三行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知 ,求
,求 的值;
的值;
(Ⅱ)设 ,求
,求 .
.
(本小题满分12分)
已知函数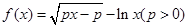 是增函数.
是增函数.
(I)求实数p的取值范围;
(II)设数列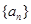 的通项公式为
的通项公式为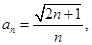 前n项和为S,求证:
前n项和为S,求证: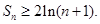
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com