
题目列表(包括答案和解析)
已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆的标准方程;
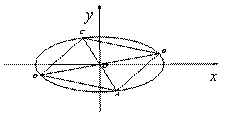
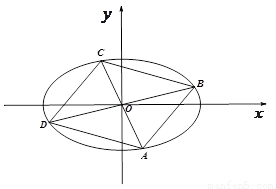
(2)四边形ABCD的顶点在椭圆上,且对角线AC、BD过原点O,若![]() , (i) 求
, (i) 求![]() 的最值.(ii)求四边形ABCD的面积;
的最值.(ii)求四边形ABCD的面积;
已知椭圆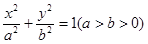 的离心率为
的离心率为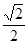 ,且过点
,且过点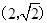 .
.
(1)求椭圆的标准方程;
(2)四边形ABCD的顶点在椭圆上,且对角线A
C、BD过原点O,若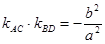 ,
,
(i)
求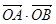 的最值.
的最值.
(ii) 求证:四边形ABCD的面积为定值;
已知椭圆 的离心率为
的离心率为 ,且过点
,且过点 .
.
(1)求椭圆的标准方程;
(2)四边形ABCD的顶点在椭圆上,且对角线A C、BD过原点O,若 ,
,
(i) 求 的最值.
的最值.
(ii) 求证:四边形ABCD的面积为定值;
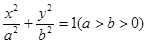 的离心率为
的离心率为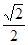 ,且过点
,且过点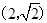 .
.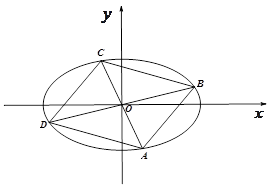
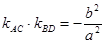 ,
,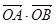 的最值.
的最值.已知椭圆 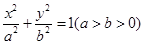 的离心率为
的离心率为  ,且过点
,且过点 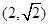
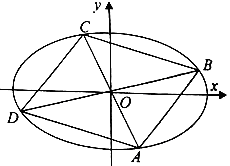
(Ⅰ)求椭圆的标准方程;
(Ⅱ)四边形ABCD的顶点在椭圆上,且对角线AC、BD过原点O,若 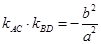 .
.
(i)求 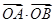 的最值:
的最值:
(i i)求证:四边形ABCD的面积为定值.
理科部分
一、选择题(本大题共12小题,每小题5分,共60分)
BAACA CDBCD AC
二、填空题(本大题共4小题,每小题4分,共16分)
13.25 14..files\image256.gif) 15.8
16.
15.8
16..files\image258.gif)
三、解答题
17.(本小题满分12分)
解:(I).files\image260.gif)
.files\image262.gif)
(Ⅱ).files\image264.gif)
.files\image266.gif)
18.(本小题满分12分)
解:(I)依题意,每场比赛获得的门票收入数组成首项为40,公差为10的等差数列,
设此数列为.files\image075.gif) ,则易知
,则易知.files\image269.gif)
.files\image271.gif)
.files\image273.gif) 此次决赛共比赛了5场。
此次决赛共比赛了5场。
(Ⅱ)由.files\image275.gif)
.files\image273.gif) 若要获得的门票收入不少于390万元,则至少要比赛6场。
若要获得的门票收入不少于390万元,则至少要比赛6场。
①若比赛共进行了6场,则前5场比赛的比分必为2:3,且第6场比赛为领先一场的
球队获胜,其概率.files\image278.gif)
②若比赛共进行了7场,则前6场胜负为3:3,则概率.files\image280.gif)
.files\image273.gif) 门票收入不少于390万元的概率为
门票收入不少于390万元的概率为.files\image283.gif)
.files\image285.jpg)
19.(本小题满分12分)
解:方法一(向量法);
(I)证明:以.files\image171.gif) 点为原点,棱
点为原点,棱.files\image288.gif) 所
所
在的直线分别为.files\image033.gif) 轴和
轴和.files\image291.gif) 轴建立空间直角坐标系
轴建立空间直角坐标系
(右手系),设.files\image293.gif) ,则
,则.files\image295.gif) ,
,.files\image297.gif)
又已知.files\image199.gif) ,
,.files\image273.gif) 可求得以下各点的
可求得以下各点的
坐标为.files\image301.gif)
.files\image303.gif)
(Ⅱ).files\image305.gif) 已知
已知.files\image195.gif) 是直四棱柱,
是直四棱柱,.files\image273.gif)
.files\image309.gif)
.files\image311.gif) ,又由(I)知
,又由(I)知.files\image211.gif) ,
,.files\image273.gif)
.files\image315.gif)
.files\image317.gif) 即是平面
即是平面.files\image319.gif) 的法向量。
的法向量。
设平面.files\image321.gif) 的法向量为
的法向量为.files\image323.gif) 则
则.files\image325.gif) 且
且.files\image327.gif)
.files\image254.jpg)
.files\image329.gif)
由图形可知,二面角.files\image213.gif) 的平面为锐角,
的平面为锐角,
.files\image273.gif) 二面角
二面角.files\image213.gif) 的大小为
的大小为 .files\image334.gif)
方法二(综合法):
(I).files\image336.gif) 是直四棱柱,
是直四棱柱,.files\image273.gif)
.files\image309.gif)
.files\image340.gif)
(Ⅱ)在.files\image342.gif) 内,过
内,过.files\image344.gif) 点作
点作.files\image346.gif) 的垂线, 交
的垂线, 交.files\image348.gif) 点,连结
点,连结.files\image350.gif) 。
。
由(I)知.files\image352.gif)
垂线定理知,.files\image354.gif)
.files\image356.gif) 就是二面角
就是二面角.files\image213.gif) 的平面角。
的平面角。.files\image254.jpg)
同(I)一样,不妨设.files\image359.gif)
在.files\image361.gif) 内,
内,.files\image363.gif)
.files\image273.gif) 二面角
二面角.files\image213.gif) 的大小为
的大小为.files\image367.gif)
20.(本小题满分12分)
解:(I).files\image369.gif)
令.files\image371.gif)
显然当.files\image373.gif)
.files\image375.gif)
(Ⅱ)①当.files\image377.gif) 时,
时, .files\image305.gif) 函数
函数.files\image223.gif) 在
在.files\image381.gif) 上是单调减函数,
上是单调减函数,
.files\image383.gif)
在.files\image385.gif) 上的最小值 ,
上的最小值 , .files\image387.gif)
又.files\image389.gif)
综上,对任意.files\image391.gif)
本问也可以这样证:
(Ⅱ).files\image305.gif) 函数
函数.files\image223.gif) 在
在.files\image395.gif) 上单调递增,在
上单调递增,在.files\image397.gif) 和
和.files\image381.gif) 上单调递减,
上单调递减,
.files\image400.gif)
.files\image273.gif) 对任意
对任意.files\image391.gif)
21.(本小题满分12分)
解:(I)设椭圆.files\image175.gif) 的方程为
的方程为.files\image404.gif)
.files\image406.gif)
.files\image273.gif) 椭圆方程化为
椭圆方程化为.files\image409.gif) 将点
将点.files\image233.gif) 代入,解得
代入,解得.files\image412.gif) ,
,.files\image273.gif) 椭圆
椭圆.files\image175.gif) 的方程为
的方程为.files\image416.gif)
(Ⅱ)显然,直线.files\image236.gif) 存在斜率(否则不满足题意,5分),设其斜率为
存在斜率(否则不满足题意,5分),设其斜率为.files\image025.gif) ,则直线
,则直线.files\image236.gif) 的方程为
的方程为.files\image421.gif) 。代入椭圆
。代入椭圆.files\image175.gif) 的方程,消去
的方程,消去.files\image161.gif) 并整理得
并整理得
.files\image425.gif)
.files\image254.jpg)
由方程判别式.files\image427.gif) , 得
, 得.files\image429.gif) ①
①
设.files\image431.gif) 两点的坐标为
两点的坐标为.files\image433.gif) ,则由韦达定理得
,则由韦达定理得
.files\image435.gif)
.files\image437.gif)
.files\image439.gif) 将上面使用韦达定理所得的结果代入,并去分
将上面使用韦达定理所得的结果代入,并去分
母整理(注意在方程两边先约去9可以简化计算)得
.files\image441.gif)
检验①式,均符合;再检验当.files\image443.gif) 时,直线
时,直线.files\image236.gif) 是否与椭圆
是否与椭圆.files\image175.gif) 相交于左右两个顶点,显然直线
相交于左右两个顶点,显然直线.files\image447.gif) 过椭圆
过椭圆.files\image175.gif) 的右顶点。
的右顶点。
.files\image450.gif) 不满足题意,舍去
不满足题意,舍去 .files\image452.gif)
.files\image273.gif) 直线
直线.files\image236.gif) 的方程为
的方程为.files\image456.gif)
22.(本小题满分14分)
解:(I)方法一:当.files\image458.gif) 时,显然由已知可得
时,显然由已知可得.files\image250.gif) 成立。
成立。
假设.files\image461.gif) 时
时.files\image250.gif) 成立,即
成立,即.files\image464.gif)
则当.files\image466.gif) 时,根据题意有
时,根据题意有.files\image468.gif)
.files\image470.gif)
.files\image273.gif) 当
当.files\image466.gif) 时,
时,.files\image250.gif) 成立。
成立。
根据数学归纳法可知,对任意.files\image475.gif) ,
,.files\image250.gif) 成立
成立.files\image254.jpg)
方法二:
.files\image478.gif)
……,.files\image480.gif) , 将这
, 将这.files\image482.gif) 个等式累乘(相乘),得
个等式累乘(相乘),得.files\image484.gif)
.files\image273.gif) 将
将.files\image487.gif) 代入得
代入得 .files\image489.gif)
.files\image273.gif)
.files\image492.gif)
检验当.files\image458.gif) 时,上式也成立,
时,上式也成立, .files\image495.gif)
方法三:
.files\image497.gif)
.files\image499.gif)
.files\image501.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com