
题目列表(包括答案和解析)
 的值,可令
的值,可令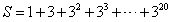 …………………① 将①式两边同乘以3,得( )…………………② ,由②减去①式,得S=( )。
…………………① 将①式两边同乘以3,得( )…………………② ,由②减去①式,得S=( )。 ,从第二项开始每一项与前一项之比的常数为q,则an=( )。 (用含
,从第二项开始每一项与前一项之比的常数为q,则an=( )。 (用含 的代数式表示),如果这个常数
的代数式表示),如果这个常数 ,那么
,那么 ( )(用含
( )(用含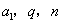 的代数式表示).
的代数式表示). | 1 |
| m |
| 1 |
| n |

| 1 |
| 8 |
| x |
| y |
| 1 |
| 2 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com