（本题满分14分）

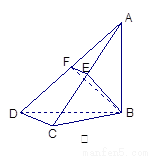
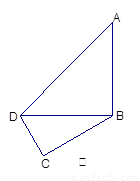
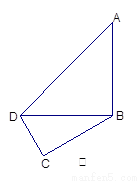
如图甲，在平面四边形ABCD中，已知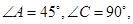

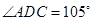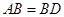,,现将四边形ABCD沿BD折起，

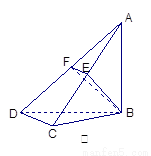
使平面ABD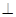平面BDC（如图乙），设点E、F分别为棱

AC、AD的中点.

（1）求证：DC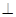平面ABC；

（2）求BF与平面ABC所成角的正弦；

（3）求二面角B－EF－A的余弦.

（本题满分14分）

如图甲，在平面四边形ABCD中，已知

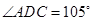,,现将四边形ABCD沿BD折起，

使平面ABD平面BDC（如图乙），设点E、F分别为棱

AC、AD的中点.

（1）求证：DC平面ABC；

（2）求BF与平面ABC所成角的正弦；

（3）求二面角B－EF－A的余弦.

（本题满分14分）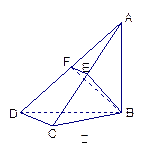

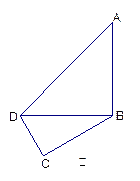
如图甲，在平面四边形ABCD中，已知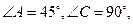
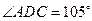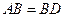,,现将四边形ABCD沿BD折起，
使平面ABD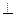平面BDC（如图乙），设点E、F分别为棱
AC、AD的中点.
（1）求证：DC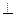平面ABC；
（2）求BF与平面ABC所成角的正弦；
（3）求二面角B－EF－A的余弦.

（本题满分14分）

如图甲，在平面四边形ABCD中，已知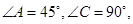

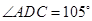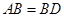,,现将四边形ABCD沿BD折起，

使平面ABD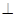平面BDC（如图乙），设点E、F分别为棱

AC、AD的中点.

（1）求证：DC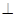平面ABC；

（2）求BF与平面ABC所成角的正弦；

（3）求二面角B－EF－A的余弦.

．（本小题满分14分）甲乙两人连续年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图：

甲调查表明：每个鱼池平均产量从第年万只鳗鱼上升到第年万只。

乙调查表明：全县鱼池总个数由第年个减少到第年个。

（1）求第年全县鱼池的个数及全县出产的鳗鱼总数；

（2）哪一年的规模(即总产量)最大?请说明理由.