
题目列表(包括答案和解析)
(本小题满分12分)w。w-w*k&s%5¥u
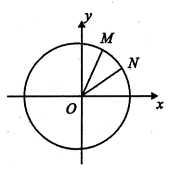 如图,在平面直角坐标系xoy中,以ox轴为始边做两个锐角
如图,在平面直角坐标系xoy中,以ox轴为始边做两个锐角![]() ,且
,且![]() 的终边依次与单位圆O相交于M、N两点,己知M、N的横坐标分别为
的终边依次与单位圆O相交于M、N两点,己知M、N的横坐标分别为![]() .、
.、![]() .
.
(I) 求![]() _的值;
_的值;
(II) 在,![]() 中,A、B为锐角,
中,A、B为锐角,![]() ,角A、B、C所对的边分别为a、b、c,若 ,
,角A、B、C所对的边分别为a、b、c,若 ,![]() ,当
,当![]() 时,求a、b、c的值.
时,求a、b、c的值.
(2009宁夏海南卷文)(本小题满分12分)
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(Ⅰ)A类工人中和B类工人各抽查多少工人?w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅱ)从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
| 生产能力分组 |
|
|
|
|
|
| 人数 | 4 | 8 |
| 5 | 3 |
表2:
| 生产能力分组 |
|
|
|
|
| 人数 | 6 | y | 36 | 18 |
先确定![]() ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)

(ii)分别估计![]() 类工人和
类工人和![]() 类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
(本小题满分12分)如图,在直三棱柱ABC―A1B1C1中,∠ACB = 90°. AC = BC = a,
D、E分别为棱AB、BC的中点, M为棱AA1上的点,二面角M―DE―A为30°.
(1)求MA的长;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)求点C到平面MDE的距离。

()(本小题满分12分)w.w.w.k.s.5.u.c.o.m ![]()
![]()
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1
(Ⅰ)证明:AB=AC w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小
(本小题满分12分)K^S*5U.C#O%M
如图,点A,B分别是椭圆![]() 的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:
的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:![]() 且
且![]() 。
。
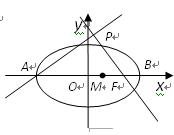
⑴求直线AP的方程;
⑵设点M是椭圆长轴AB上一点,点M到直线AP的距离等于![]() ,求椭
,求椭![]() 圆上的点到K^S*5U.C#O%M
圆上的点到K^S*5U.C#O%M
点M的距离d的最小值![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com