题目列表(包括答案和解析)
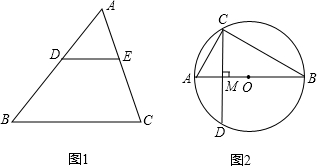（1）如图1在△ABC中，D为AB上一点，DE∥BC交AC于点E，若AD：DB=2：3，BC=10，求DE的长．
（1）如图1，AB为圆O的直径，弦CD⊥AB，垂足为点E，连接OC，若AB=10，CD=8，求AE的长． | AC |
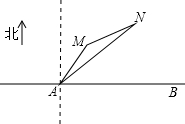（2013•南充）如图，公路AB为东西走向，在点A北偏东36.5°方向上，距离5千米处是村庄M；在点A北偏东53.5°方向上，距离10千米处时村庄N（参考数据；sin36.5°=0.6，cos36.5°=0.8，tan36.5°=0.75）．一、1．C 2．D 3．C 4．B 5．C 6．A 7．C 8．D 9. C 10. A
二、11．
12．
13．62° 14．4 15．(n+2)2-4n=n2+4 16．25
17．5 18．15°或75°
三、19．原式=a2+a-(a2-1)
……（3分）
=a2+a-a2+1 ……（6分）
=a+1 ……（9分）
20．（1）画图如图所示； ……（4分）
（2）点A/的坐标为（-2,4）； ……（7分）
（3）
的长为：
. ……（10分）
21．（1）设小明他们一共去了x个成人，则去了学生(12-x)人，依题意，得
35x+0.5×35(12-x)=350 ………………………………（3分）
解这个方程，得x=8 ………………………………（5分）
答：小明他们一共去了8个成人，去了学生4人. ……………………（6分）
（2）若按16个游客购买团体票，需付门票款为35×0.6×16=336(元) ……（8分）
∵ 336＜350， ………………………………（9分）
∴ 按16人的团体购票更省钱.
………………………………（10分）
22．（1）李华所在班级的总人数为：
14÷35%=40(人). ……（3分）
爱好书画的人数为：
40-
（2）书画部分的条形图如图所示.（9分）
（3）答案不唯一.（每写对一条给1分）如：表示“球类”的扇形圆心角为：
360×
=126°爱好音乐的人数是其他爱好人数的3倍等. …………（11分）
23．（1）由图象可知公司从第4个月末以后开始扭亏为盈. ………………………（2分）
（2）由图象可知其顶点坐标为(2,-2)，
故可设其函数关系式为：y=a(t-2)2-2. ………………………………（4分）
∵ 所求函数关系式的图象过(0,0)，于是得
a(0-2)2-2=0，解得a=
.
………………………………（5分）
∴ 所求函数关系式为：S=(t-2)2-2或S=t2-2t. ………………………（7分）
（3）把t=7代入关系式，得S=×72-2×7=10.5 ……………………………（10分）
把t=8代入关系式，得S=×82-2×8=16
16-10.5=5.5 ………………………………（11分）
答：第8个月公司所获利是5.5万元. ………………………………（12分）
24．（1）∵ BC、DE分别是两个等腰直角△ADE、△ABC的斜边，
∴ ∠DAE=∠BAC=90°，
∴ ∠DAE-∠DAC=∠BAC-∠DAC，∴ ∠CAE=∠BAD. ………………（2分）
在△ACE和△ABD中，
………………………………（4分）
∴ △ACE≌△ABD（S?A?S）. ………………………………（5分）
（2）①∵ AC=AB=
，
∴ BC=AC2+AB2=
，
∴ BC=4. ………………………………（6分）
∵ AB=AC, ∠BAC=90°,
∴ ∠ACB=∠B=45°，
∵ △ACE≌△ABD
∴ ∠ACB=∠B=45°
∴ ∠DCE=90°. ………………………………（7分）
∵ △ACE≌△ABD,
∴ CE=BD=x，而BC=4，∴ DC=4-x，
∴ Rt△DCE的面积为DC?CE=(4-x)x.
∴ (4-x)x=1.5
………………………………（9分）
即x2-4x+3=0. 解得x=1或x=3. ………………………………（11分）
② △DCE存在最大值，理由如下：
设△DCE的面积为y，于是得y与x的函数关系式为：
y=(4-x)x (0＜x＜4)
………………………………（12分）
=-(x-2)2+2
∵ a=-＜0, ∴ 当x=2时，函数y有最大值2. ……………………（13分）
又∵ 此时，x满足关系式0＜x＜4，
故当x=2时，△DCE的最大面积为2. ………………………………（14分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com