
题目列表(包括答案和解析)
 一个带电微粒在图示的正交匀强电场和匀强磁场中在竖直面内做匀速圆周运动.则该带电微粒必然带
一个带电微粒在图示的正交匀强电场和匀强磁场中在竖直面内做匀速圆周运动.则该带电微粒必然带| gBr |
| E |
| gBr |
| E |
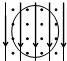
一个带电微粒在图示的正交匀强电场和匀强磁场中在竖直面内做匀速圆周运动。则该带电微粒必然带_____,旋转方向为_____。若已知圆半径为r,电场强度为E磁感应强度为B,则线速度为_____。

一个带电微粒在图示的正交匀强电场和匀强磁场中在竖直面内做匀速圆周运动。则该带电微粒必然带_____,旋转方向为_____。若已知圆半径为r,电场强度为E磁感应强度为B,则线速度为_____。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com