题目列表(包括答案和解析)
C．选修4-4：坐标系与参数方程
在极坐标系下，已知圆O：
和直线
，
（1）求圆O和直线
的直角坐标方程；（2）当
时，求直线与圆O公共点的一个极坐标.
D．选修4-5：不等式证明选讲
对于任意实数
和
，不等式
恒成立，试求实数
的取值范围．
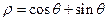和直线
，
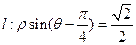的直角坐标方程；（2）当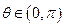
时，求直线与圆O公共点的一个极坐标.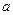
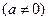和
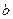，不等式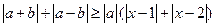
恒成立，试求实数
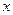的取值范围．C
[解析] 由基本不等式，得ab≤
＝
＝
－ab，所以ab≤
，故B错；
＋
＝
＝
≥4，故A错；由基本不等式得
≤
＝
，即
＋
≤
，故C正确；a2＋b2＝(a＋b)2－2ab＝1－2ab≥1－2×＝，故D错．故选C.
．定义域为R的函数
满足
，且当
时，
，则当
时，
的最小值为（ ）
（A）
（B）
（C）
（D）
．过点
作圆
的弦，其中弦长为整数的共有 （ ）
A.16条 B. 17条 C. 32条 D. 34条
一、选择题（本大题共12个小题，每小题5分，共60分）
1―5 CABDC 6―10 DCCBB 11―12AB
二、填空题：
13．9
14．
15．（1，0）
16．420
三、解答题：
17．解：（1）
（2）由（1）知，
18．解： 记“第i个人过关”为事件Ai（i=1，2，3），依题意有
。
（1）设“恰好二人过关”为事件B，则有
，
且
彼此互斥。
于是
=
（2）设“有人过关”事件G，“无人过关”事件
互相独立，
19．解法：1：（1）
（2）过E作EF⊥PC，垂足为F，连结DF。 （8分）
|
解得
（6分）
，列表如下：
因为直线l与椭圆交点在y轴右侧，
解得2
。
（4分）
得
（λ≠0）。 （9分）
解得
（14分）
