
题目列表(包括答案和解析)
(2009江苏卷)(本小题满分16分)
按照某学者的理论,假设一个人生产某产品单件成本为![]() 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() ;如果他买进该产品的单价为
;如果他买进该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为![]() 和
和![]() ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为![]() .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为![]() 元和
元和![]() 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为![]() ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为![]()
(1)求![]() 和
和![]() 关于
关于![]() 、
、![]() 的表达式;当
的表达式;当![]() 时,求证:
时,求证:![]() =
=![]() ;
;
(2)设![]() ,当
,当![]() 、
、![]() 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
(3)记(2)中最大的综合满意度为![]() ,试问能否适当选取
,试问能否适当选取![]() 、
、![]() 的值,使得
的值,使得![]() 和
和![]() 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
已知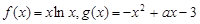
(1)求函数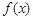 在
在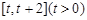 上的最小值
上的最小值
(2)对一切的 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(3)证明对一切 ,都有
,都有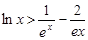 成立
成立
【解析】第一问中利用
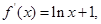 当
当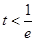 时,
时,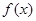 在
在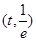 单调递减,在
单调递减,在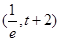 单调递增
单调递增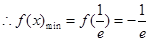 ,当
,当
 ,即
,即 时,
时,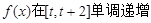 ,
,
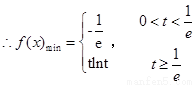
第二问中,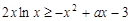 ,则
,则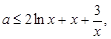 设
设 ,
,
则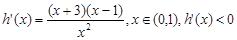 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,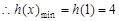 ,因为对一切
,因为对一切 ,
,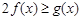 恒成立,
恒成立,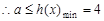
第三问中问题等价于证明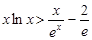 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则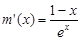 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
解:(1)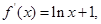 当
当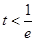 时,
时,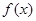 在
在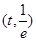 单调递减,在
单调递减,在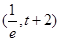 单调递增
单调递增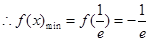 ,当
,当
 ,即
,即 时,
时,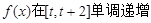 ,
,
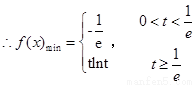 …………4分
…………4分
(2)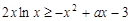 ,则
,则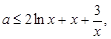 设
设 ,
,
则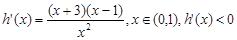 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,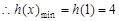 ,因为对一切
,因为对一切 ,
,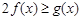 恒成立,
恒成立,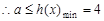 …………9分
…………9分
(3)问题等价于证明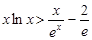 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则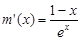 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
如图,有三个并排放在一起的正方形,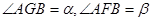 .
.
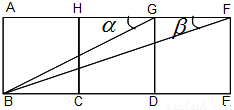
(1)求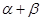 的度数;
的度数;
(2)求函数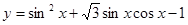 的最大值及取得最大值时候的x值。
的最大值及取得最大值时候的x值。
【解析】本试题主要是考查了三角函数的两角和差的三角公式的运用以及三角函数性质的综合运用。
(1)妨设正方形边长为1,易知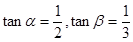 ,可得
,可得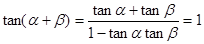 得到结论。
得到结论。
(2)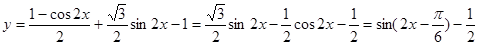 可知y的最大值,进而得到x的取值集合。
可知y的最大值,进而得到x的取值集合。
(本小题满分13分)
古汉集团生产的A,B两种型号的口服液供出口,国家为鼓励产品出口,采用出口退税政策:出口价值为a万元的/1产品可获得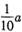 万元的退税款,出口价值为b万元的B产品可获得
万元的退税款,出口价值为b万元的B产品可获得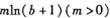 万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.
万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.
(1) 当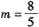 时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;(精确到0.1,参考数据:
时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;(精确到0.1,参考数据: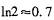 )
)
(2) 记该企业获得的退税款的最大值函数为,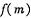 ,求
,求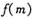 的表达式.
的表达式.
(本小题满分13分)
古汉集团生产的A,B两种型号的口服液供出口,国家为鼓励产品出口,采用出口退税政策:出 口价值为a万元的/1产品可获得
口价值为a万元的/1产品可获得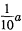 万元的退税款,出口价值为b万元的B产品可获得
万元的退税款,出口价值为b万元的B产品可获得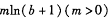 万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.
万元的退税款.已知厂家出口总价值为100万元的A、B两种口服液,且两种口服液的出口价值都不低于10万元.
(1) 当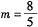 时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;(精确到0.1,参考数据:
时,请你制定一个方案,使得在这次出口贸易中该企业获得的退税款最多,并求出其最大值;(精确到0.1,参考数据: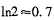 )
)
(2) 记该企业获得的退税款的最大值函数为, ,求
,求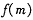 的表达式.
的表达式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com