设函数f(x)＝sin(ωx＋)(其中ω＞0，||＜)，给出五个论断：

①它的图象关于直线x＝对称；

②它的图象关于点(，0)对称；

③它的周期是π；

④它在区间[－，0]上是增函数；

⑤过点(0，)．

以上其中两个论断作为条件，其余三个认断作为结论，写出你认为正确的一个命题，则该命题是________．

解答题：要求写出文字说明、证明过程和演算步骤

在三棱锥S－ABC中，侧面SAC⊥底面ABC，△SAC是边长为4的正三角形，△ACB为直角三角形，∠ACB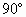＝，BC＝4．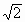

(Ⅰ)求证：侧面SAC⊥侧面BSC；

(Ⅱ)求SB与底面ABC所成角；

(Ⅲ)求二面角S—AB—C的正切值．

已知函数f(t)满足对任意实数x，y都有f(x＋y)＝f(x)＋f(y)＋xy＋1，且f(－2)＝－2，

(1)求f(1)的值．

(2)证明：对于一切大于1的正整数t，恒有f(t)＞t．

(3)试求满足f(t)＝t的整数t的个数，并说明理由．

t∈R，t∈(0，10)，由t确定两个任意点P(t，t)，Q(10－t，0)．问：①直线PQ是否能通过下面的点M(6，1)，N(4，5)；②在△OPQ内作内接正方形ABCD，顶点A、B在边OQ上，顶点C在边PQ上，顶点D在边OP上．

(1)求证：顶点C一定在直线y＝x上．

(2)求下图中阴影部分面积的最大值，并求这时顶点A、B、C、D的坐标．

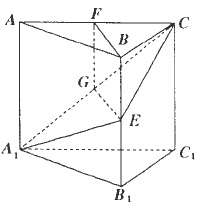
如下图所示，在正三棱柱ABC－A₁B₁C₁中，E∈BB₁，截面A₁EC⊥侧面AC₁

(1)求证：BE＝EB₁；

(2)若AA₁＝A₁B₁，求平面A₁EC与平面A₁B₁C₁所成的锐二面角的度数．