
题目列表(包括答案和解析)
解关于 的不等式:
的不等式:

【解析】解:当 时,原不等式可变为
时,原不等式可变为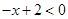 ,即
,即 (2分)
(2分)
当 时,原不等式可变为
时,原不等式可变为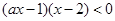
 (5分) 若
(5分) 若 时,
时, 的解为
的解为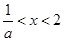 (7分)
(7分)
若 时,
时, 的解为
的解为 (9分) 若
(9分) 若 时,
时, 无解(10分) 若
无解(10分) 若 时,
时, 的解为
的解为 (12分综上所述
(12分综上所述
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为:
时,原不等式的解为: 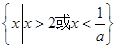
已知二次函数![]() 的图像经过坐标原点,且满足
的图像经过坐标原点,且满足![]() ,设函数
,设函数![]() ,其中
,其中![]() 为非零常数
为非零常数
(I)求函数![]() 的解析式;
的解析式;
(II)当![]() 时,判断函数
时,判断函数![]() 的单调性并且说明理由;
的单调性并且说明理由;
(III)证明:对任意的正整数![]() ,不等式
,不等式![]() 恒成立
恒成立
古希腊数学家丢番图(公元250年前后)在《算术》中就提到了一元二次![]() 方程的问题,不过当时古希腊人还没有寻求到它的求根公式,只能用图解等方法来求解。在欧几里得的《几何原本》中,形如
方程的问题,不过当时古希腊人还没有寻求到它的求根公式,只能用图解等方法来求解。在欧几里得的《几何原本》中,形如![]() (a>0,b>0)的方程的图解法是:如图,以
(a>0,b>0)的方程的图解法是:如图,以![]() 和b为两直角边做Rt△ABC,再在斜边上截取
和b为两直角边做Rt△ABC,再在斜边上截取![]() ,则AD的长就是所求方程的解。
,则AD的长就是所求方程的解。
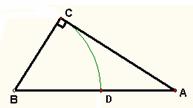
(1)请用含字母a、b的代数式表示AD的长。
(2)请利用你已学的知识说明该图解法的正确性,并说说这种解法的遗憾之处。
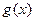 的图像经过坐标原点,且满足
的图像经过坐标原点,且满足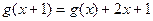 ,设函数
,设函数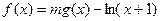 ,其中
,其中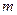 为非零常数
为非零常数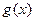 的解析式;
的解析式;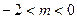 时,判断函数
时,判断函数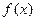 的单调性并且说明理由;
的单调性并且说明理由;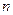 ,不等式
,不等式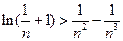 恒成立
恒成立关于
x的不等式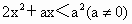 ,提供四个解集:①当a>0时,
,提供四个解集:①当a>0时,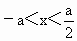 ,②当a>0时,
,②当a>0时,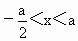 ,③当a<0时,
,③当a<0时,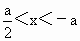 ,④当a<0时,
,④当a<0时,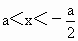 ,那么原不等式的解集为
,那么原不等式的解集为
[
]|
A .②或③ |
B .①或③ |
C .①或④ |
D .②或④ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com