
题目列表(包括答案和解析)
已知二次函数![]() 同时满足:①不等式
同时满足:①不等式![]() ≤0的解集有且只有一个元素;②在定义域内存在
≤0的解集有且只有一个元素;②在定义域内存在![]() ,使得不等式
,使得不等式![]() 成立,设数列{
成立,设数列{![]() }的前
}的前![]() 项和
项和![]() .
.
(1)求函数![]() 的表达式;
的表达式;
(2) 设各项均不为0的数列{![]() }中,所有满足
}中,所有满足![]() 的整数
的整数![]() 的个数称为这个数列{
的个数称为这个数列{![]() }的变号数,令
}的变号数,令![]() (
(![]()
![]() ),求数列{
),求数列{![]() }的变号数;
}的变号数;
(3)设数列{![]() }满足:
}满足:![]() ,试探究数列{
,试探究数列{![]() }是否存在最小项?若存在,求出该项,若不存在,说明理由.
}是否存在最小项?若存在,求出该项,若不存在,说明理由.
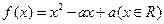 同时满足:①不等式
同时满足:①不等式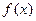 ≤0的解集有且只有一个元素;②在定义域内存在
≤0的解集有且只有一个元素;②在定义域内存在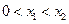 ,使得不等式
,使得不等式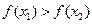 成立,设数列{
成立,设数列{ }的前
}的前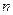 项和
项和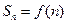 .
.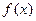 的表达式;
的表达式;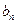 }中,所有满足
}中,所有满足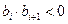 的整数
的整数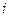 的个数称为这个数列{
的个数称为这个数列{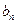 }的变号数,令
}的变号数,令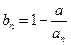 (
(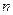
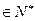 ),求数列{
),求数列{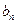 }的变号数;
}的变号数; 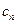 }满足:
}满足: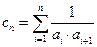 ,试探究数列{
,试探究数列{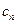 }是否存在最小项?若存在,求出该项,若不存在,说明理由.
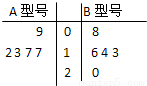
}是否存在最小项?若存在,求出该项,若不存在,说明理由.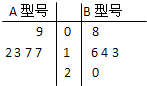 某工厂生产A、B两种型号的产品,每种型号的产品在出厂时按质量分为一等品和二等品.为便于掌握生产状况,质检时将产品分为每20件一组,分别记录每组一等品的件数.现随机抽取了5组的质检记录,其一等品数茎叶图如图所示:
某工厂生产A、B两种型号的产品,每种型号的产品在出厂时按质量分为一等品和二等品.为便于掌握生产状况,质检时将产品分为每20件一组,分别记录每组一等品的件数.现随机抽取了5组的质检记录,其一等品数茎叶图如图所示:| 等级 利润 产品 |
一等品 | 二等品 |
| A型 | 4(万元) | 3(万元) |
| B型 | 3(万元) | 2(万元) |
| 项目 用量 产品 |
配件(件) | 资金(万元) |
| A型 | 6 | 4 |
| B型 | 2 | 8 |
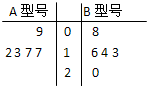 某工厂生产A、B两种型号的产品,每种型号的产品在出厂时按质量分为一等品和二等品.为便于掌握生产状况,质检时将产品分为每20件一组,分别记录每组一等品的件数.现随机抽取了5组的质检记录,其一等品数茎叶图如图所示:
某工厂生产A、B两种型号的产品,每种型号的产品在出厂时按质量分为一等品和二等品.为便于掌握生产状况,质检时将产品分为每20件一组,分别记录每组一等品的件数.现随机抽取了5组的质检记录,其一等品数茎叶图如图所示:| 等级 利润 产品 | 一等品 | 二等品 |
| A型 | 4(万元) | 3(万元) |
| B型 | 3(万元) | 2(万元) |
| 表二 |
| 表二 |
| 项目 用量 产品 | 配件(件) | 资金(万元) |
| A型 | 6 | 4 |
| B型 | 2 | 8 |
| 等级 利润 产品 | 一等品 | 二等品 |
| A型 | 4(万元) | 3(万元) |
| B型 | 3(万元) | 2(万元) |
| 表二 |
| 表二 |
| 项目 用量 产品 | 配件(件) | 资金(万元) |
| A型 | 6 | 4 |
| B型 | 2 | 8 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com