
题目列表(包括答案和解析)
(本小题满分12分)已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
,
(1)确定函数 的解析式;
的解析式;
(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)解不等式 .
.
【解析】第一问利用函数的奇函数性质可知f(0)=0
结合条件 ,解得函数解析式
,解得函数解析式
第二问中,利用函数单调性的定义,作差变形,定号,证明。
第三问中,结合第二问中的单调性,可知要是原式有意义的利用变量大,则函数值大的关系得到结论。
 阅读以下程序语句,若希望输出s=55,则应将条件i≥8改为
阅读以下程序语句,若希望输出s=55,则应将条件i≥8改为(本小题满分12分)有一批货物需要用汽车从城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响.据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:所用的时间(天数)

(I)为进行某项研究,从所用时间为12天的60辆汽车中随机抽取6辆.
(i) 若用分层抽样的方法抽取,求从通过公路1和公路2的汽车中各抽取几辆;
(ii)若从(i)的条件下抽取的6辆汽车中,再任意抽取两辆汽车,求这两辆汽车至少有一辆通过公路1的概率.
(II)假设汽车4只能在约定日期(某月某日)的前11天出发,汽车1只能在约定日期的前12天出发.为了尽最大可能在各自允许的时间内将货物运往城市乙,估计汽车4和汽车S应如何选择各自的路径.
某种产品按质量标准分成五个等级,等级编号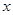 依次为1,2,3,4,5.现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
依次为1,2,3,4,5.现从一批产品中随机抽取20件,对其等级编号进行统计分析,得到频率分布表如下:
|
|
1 |
2 |
3 |
4 |
5 |
|
频率 |
|
0.2 |
0.45 |
|
|
(I)若所抽取的20件产品中,等级编号为4的恰有3件,等级编号为5的恰有2件,求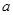 ,
,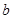 ,
,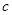 的值;
的值;
(Ⅱ)在(I)的条件下,将等级编号为4的3件产品记为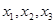 ,等级编号为5的2件产品记为
,等级编号为5的2件产品记为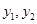 ,现从
,现从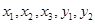 这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件产品的等级编号恰好相同的概率.
这5件产品中任取两件(假定每件产品被取出的可能性相同),写出所有可能的结果,并求这两件产品的等级编号恰好相同的概率.
袋子中装有大小形状完全相同的m个红球和n个白球,其中m,n满足m>n≥2且m+n≤l0(m,n∈N+),若从中取出2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.
(Ⅰ) 求m,n的值;
(Ⅱ) 从袋子中任取3个球,设取到红球的个数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
【解析】第一问中利用 ,解得m=6,n=3.
,解得m=6,n=3.
第二问中, 的取值为0,1,2,3. P(
的取值为0,1,2,3. P( =0)=
=0)= 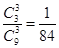 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
得到分布列和期望值
解:(I)据题意得到 解得m=6,n=3.
解得m=6,n=3.
(II) 的取值为0,1,2,3.
的取值为0,1,2,3.
P( =0)=
=0)= 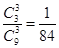 , P(
, P( =1)=
=1)= 
P( =2)=
=2)=  , P(
, P( =3)=
=3)= 
 的分布列为
的分布列为

所以E =2
=2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com