
题目列表(包括答案和解析)
在 中,满足
中,满足 ,
, 是
是 边上的一点.
边上的一点.
(Ⅰ)若 ,求向量
,求向量 与向量
与向量 夹角的正弦值;
夹角的正弦值;
(Ⅱ)若 ,
, =m (m为正常数) 且
=m (m为正常数) 且 是
是 边上的三等分点.,求
边上的三等分点.,求 值;
值;
(Ⅲ)若 且
且 求
求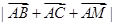 的最小值。
的最小值。
【解析】第一问中,利用向量的数量积设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则 为所求
为所求
第二问因为 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则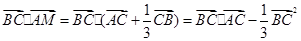 =
=
(2)当 时,则
时,则 =
=
第三问中,解:设 ,因为
,因为
 ,
, ;
;
所以 即
即 于是
于是 得
得
从而
运用三角函数求解。
(Ⅰ)解:设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则 为所求……………2分
为所求……………2分
(Ⅱ)解:因为 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则 =
= ;-2分
;-2分
(2)当 时,则
时,则 =
= ;--2分
;--2分
(Ⅲ)解:设 ,因为
,因为
 ,
, ;
;
所以 即
即 于是
于是 得
得
从而 ---2分
---2分
= =
=
= …………………………………2分
…………………………………2分
令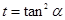 ,
, 则
则 ,则函数
,则函数 ,在
,在 递减,在
递减,在 上递增,所以
上递增,所以 从而当
从而当 时,
时,
| a+2 |
| 2 |
| 2+2 |
| 2 |
| a+2 |
| 2 |
| a+a |
| 2 |
| n |
| m |
| n0 |
| m0 |
| n0+1 |
| m0+1 |
| n0+1 |
| m0+1 |
已知二次函数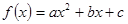
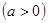 ,方程
,方程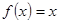 的两个根为
的两个根为 ,
,
满足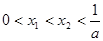 ,那么当
,那么当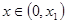 时,
时, 与
与 的大小关系为(
)
的大小关系为(
)
A 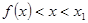 B
B
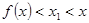 C
C
 D
D

在解决问题:“证明数集 没有最小数”时,可用反证法证明.
没有最小数”时,可用反证法证明.
假设 是
是 中的最小数,则取
中的最小数,则取 ,可得:
,可得: ,与假设中“
,与假设中“ 是
是 中的最小数”矛盾! 那么对于问题:“证明数集
中的最小数”矛盾! 那么对于问题:“证明数集 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设 是
是 中的最大数,则可以找到
中的最大数,则可以找到 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知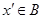 ,
, ,这与假设矛盾!所以数集
,这与假设矛盾!所以数集 没有最大数.
没有最大数.
下列叙述中正确的是( )
①反证法原理是在假设 下,如果推出一个矛盾,就证明
下,如果推出一个矛盾,就证明 不成立.
不成立.
②独立性检验原理是在假设 下,如果出现一个与
下,如果出现一个与 相矛盾的小概率事件,就推断
相矛盾的小概率事件,就推断 不成立,且该推断犯错误的概率不超过这个小概率.
不成立,且该推断犯错误的概率不超过这个小概率.
③三段论可以表示为:大前提:M是P.小前提:S是M.结 论:S是P.
④流程图常常用来表示一些动态过程,通常会有一个 “起点”,一个或多个“终点”.程序框图是流程图的一种.
A.①②③ B.①②④ C.②③④ D.①②③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com