24、为了让学生了解环保知识，增强环保意识，某中学举行了一次大规模的“环保知识竞赛”，初中三个年级共有900名学生参加了初赛，为了解本次初赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．

（一）请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：
（1）填充频率分布表中的空格：
（2）补全频率分布直方图：
（3）在该问题中的样本容量是多少？答：

50

．
（4）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？（不要求说明理由）答：

80.5-90.5

．
（5）若成绩在80分以上（不含80分）为优良，则该成绩优良的约为多少人？答：

28

．
（二）初中三个年级根据初赛成绩分别选出了10名同学参加决赛，这些选手的决赛成绩（满分为100分）如下表所示：

（6）请你填写下表：

（7）请从以下两个不同的角度对三个年级的决赛成绩进行分析：
＜1＞从平均数和众数相结合看（分析哪个年级成绩好些）．
＜2＞从平均数和中位数相结合看（分析哪个年级成绩好些）．
（8）如果在每个年级参加决赛的选手中分别选出3人参加总决赛，你认为哪个年级的实力更强一些？并说明理由．

查看答案和解析>>

查看答案和解析>>

（2010•高要市二模）为了让学生了解环保知识，增强环保意识，某中学举行了一次大规模的“环保知识竞赛”，初中三个年级共有900名学生参加了初赛，为了解本次初赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．
频数分布表

分组	频数	频率
50.5～60.5	4	0.08
60.5～70.5	8	0.16
70.5～80.5	10	0.20
80.5～90.5	16	0.32
90.5～100.5
合计

（一）请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：
（1）填充频率分布表中的空格：
（2）补全频率分布直方图：
（3）在该问题中的样本容量是多少？答：______．
（4）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？（不要求说明理由）答：______．
（5）若成绩在80分以上（不含80分）为优良，则该成绩优良的约为多少人？答：______．
（二）初中三个年级根据初赛成绩分别选出了10名同学参加决赛，这些选手的决赛成绩（满分为100分）如下表所示：

	决赛成绩（单位：分）
初一年级	80	86	88	80	88	99	80	74	91	89
初二年级	85	85	87	97	85	76	88	77	87	88
初三年级	82	80	78	78	81	96	97	88	89	86

（6）请你填写下表：

	平均数	众数	中位数
初一年级	85.5	80
初二年级	85.5		86
初三年级			84

（7）请从以下两个不同的角度对三个年级的决赛成绩进行分析：
＜1＞从平均数和众数相结合看（分析哪个年级成绩好些）．
＜2＞从平均数和中位数相结合看（分析哪个年级成绩好些）．
（8）如果在每个年级参加决赛的选手中分别选出3人参加总决赛，你认为哪个年级的实力更强一些？并说明理由．

查看答案和解析>>

查看答案和解析>>

某中学为了参加唐山市举办的“保护环境，爱我家园”演讲比赛，先在八（1）班，八（2）班分别选出10名同学进行选拔赛，这些选手的参赛成绩如图1所示：

团体	众数	平均数	方差
八（1）班		85.8	39.36
八（2）班		85.8	31.36

根据图中和上表提供的信息，解答下列问题：
（1）请你把上面的表格填写完整；
（2）请从下列不同角度对这次竞赛成绩的结果进行分析：
①从众数和平均数的角度比较，两个班中整体成绩较好是______班；
②从平均数和方差的角度比较，两个班中整体成绩较好是______班；
（3）图2是本次选拔赛中各分数段的人数与参赛总人数的百分比统计图，其中A：95≤x＜100；B：90≤x＜95；C：85≤x＜90；D：80≤x＜85；E：75≤x＜80；x代表分数．请仿照图中已有的数据将这个统计图的其它数据补充完整．
（4）假设参加市级比赛的1名选手要在这次选拔赛中成绩高于90分的选手中产生，求这1名选手产生在八（1）班的概率．

查看答案和解析>>

选择题

1-5. CDCBA   6-8. BDC

填空题

9. －2  ;     10.   ;       11. 7  ;     12. （不唯一） .

解答题

13. 解：原式= -------------------------------------------------------------4分

           =  -----------------------------------------------------------------------------5分

14. 解： 不等式  的解集是 -----------------------------------------1分

        不等式  的解集是  -------------------------------------------------2分

        所以，此不等式组的解集是 ---------------------------------------------4分

              整数解为 ?2 ，?1 ， 0 ，1 .  --------------------------------------------5分

15. 解: 由题意,得  , ∴

       ∴ 反比例函数的解析式为 ----------------------------------------------------2分

       ∵ 点在反比例函数图象上

       ∴   ---------------------------------------------------------------------------------3分

     又∵ 一次函数的图象过点 、

       ∴ -----------------------------------------------------------------------------4分

       ∴  所以一次函数的解析式为 -----------------------------5分

16. 证明：在正方形ABCD中，∠DAF=∠ABE=90°， DA=AB.  ------------------------1分

∵DG⊥AE，

∴∠FDA +∠DAG=90°.  --------------------------------------------------------------2分

又∵∠EAB+∠DAG=90°，                         

∴∠FDA =∠EAB.  -----------------------------------------------------------------------3分

∴△DAF≌△ABE， ----------------------------------------------------------------------4分

∴DF=AE.   ------------------------------------------------------------------------------5分

17. 解：

∵

∴   ---------------------------------------------------------------------------------2分

∴   -----5分

18. 解：

（1）过点D作DE⊥OB于E，过点C作CF⊥OB于F.

∵四边形OBCD是等腰梯形，OD=BC ,

∴ Rt△ODE≌Rt△BCF ,四边形CDEF是矩形.

∴ OE=BF , DC=EF .----------------------------------------------------------------------------1分

∵ OD=BC=2, OB=5, ∠BOD=60°,

∴ OE=BF=1 ,   DC=EF=3.

∴ 梯形OBCD的周长是12 --------------------------------------------------------------------2分

(2) 设点M的坐标为 ,联结DM和CM.

  ∵ ∠BOD=∠COD=∠OBC=60°

∴ ∠ODM+∠OMD=∠BMC+∠OMD=120°

∴ ∠ODM=∠BMC --------------------------------------------------------------------------------3分

∵ △OMD∽△BCM

∴

∴   --------------------------------------------------------------------------------------4分

∴

∴ 点M的坐标为(1, 0) 或(4,0)  ----------------------------------------------------------------5分

19. 解：(1) 联结OC. ∵ PC为⊙O的切线 ,

∴ PC⊥OC .

∴ ∠PCO=90°. ----------------------------------------------------------------------1分

∵ ∠ACP=120°

∴ ∠ACO=30°

∵ OC=OA ,

∴ ∠A=∠ACO=30°.     

∴ ∠BOC=60°--------------------------------------------------------------------------2分

∵ OC=4

∴

∴ -------------------------------------------3分

(2)   ∠CMP的大小不变，∠CMP=45° --------------------------------------------------4分

          由（1）知 ∠BOC+∠OPC=90°

∵ PM平分∠APC

∴ ∠APM=∠APC

∵ ∠A=∠BOC

∴ ∠PMC=∠A+∠APM=(∠BOC+∠OPC)= 45°---------------------------5分

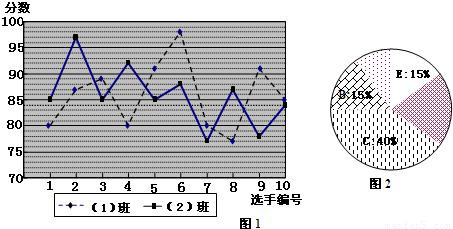
20. 解：（1）21    --------------------------------------      1分

（2）一班众数为90，二班中位数为80?????????????????????????????????????????????????????????????????????????? 3分

（3）①从平均数的角度看两班成绩一样，从中位数的角度看一班比二班的成绩好，所以一班成绩好；     4分

②从平均数的角度看两班成绩一样，从众数的角度看二班比一班的成绩好，所以二班成绩好；    5分

③从级以上（包括级）的人数的角度看，一班人数是18人，二班人数是12人，所以一班成绩好．   6分

21.解：（1）设购进甲种商品件，乙种商品件．

根据题意，得-------------------------------------------2分

 化简，得

解之，得                                                                                                             

答：该商场购进甲、乙两种商品分别为200件和120件． ------------------------------------3分

（2）甲商品购进400件，获利为（元）．

从而乙商品售完获利应不少于（元）．

设乙商品每件售价为元，则．--------------------------------------------4分

解得．所以，乙种商品最低售价为每件108元．------------------------------------5分

22.（1）由题意，

要使，须，

．

，

即时，能使得．------------------------------------------------------------2分

(2）的值的大小没有变化,  总是105°.-------------------3分

当时，总有存在．

，

又，

．

又，

．------------------------------------------------------5分

23. 解：（1）　　---------------------------------------------1分

　　　　　　　---------------------------------------------------------------------------------2分

不论取何值，方程总有两个不相等实数根　　-------------------------------------------3分

（2）由原方程可得

　∴ 　　--------------------------------------------------------------4分

 ∴  ---------------------------------------------------------------------------------5分

　又∵

　　∴　

　  ∴　　---------------------------------------------------------------------------------6分

   经检验：符合题意．

  　∴ 的值为4．　　----------------------------------------------------------------------7分

24. 解：（1）∵抛物线经过点A(2,0)， C（0，2），

            ∴    解得

            ∴抛物线解析式为 ---------------------2分

        （2） ∵点B(1,n) 在抛物线上

              ∴  -----------------------------------3分

过点B作BD⊥y轴，垂足为D.

             ∴BD=1 , CD=

             ∴ BC=2  --------------------------------------------4分

       （3） 联结OB.

在Rt△BCD中, BD=1 ,BC=2 ,

∴∠BCD=30° ----------------------------------------5分

∵ OC=BC

∴∠BOC=∠OBC

∵∠BCD=∠BOC+∠OBC

∴∠BOC=15°

∴∠BOA=75°------------------------------------------6分

过点B作BE⊥OA , 垂足为E，则OE=AE.

∴OB=AB

∴∠OAB=∠BOA=75°.-------------------------------7分

25.（1）BM=DM ，BM⊥DM  --------------------------------------------------------1分

证明：在Rt△EBC中，M是斜边EC的中点，

∴  ．

∴  ∠EMB=2∠ECB．

在Rt△EDC中，M是斜边EC的中点，

∴  ．

∴   ∠EMD=2∠ECD．-------------------2分

∴  BM=DM，∠EMD＋∠EMB =2（∠ECD＋ECB）．

∵  ∠ECD＋∠ECB=∠ACB=45°，

∴  ∠BMD=2∠ACB=90°，即BM⊥DM． -------------------------------3分

（2）当△ADE绕点A逆时针旋转小于45°的角时，  （1）中的结论成立．

证明：

连结BD，延长DM至点F，使得DM=MF，连结BF、FC，延长ED交AC于点H．

                                  -------------------------------------4分

∵ DM=MF，EM=MC，

∴ 四边形是平行四边形.

∴ DE∥CF ，ED =CF，

∵ ED= AD,

∴ AD=CF.

∵ DE∥CF，----------------------------------------5分

∴ ∠AHE=∠ACF．

∵ ,，

∴ ∠BAD=∠BCF. --------------------------------------------------6分

又∵AB= BC,

∴ △ABD≌△CBF.

∴ BD=BF，∠ABD=∠CBF.

∵ ∠ABD+∠DBC =∠CBF+∠DBC，

∴∠DBF=∠ABC =90°.

在Rt△中，由,，得BM=DM且BM⊥DM． -------7分