
题目列表(包括答案和解析)
(本小题满分13分)
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元。设1件产品的利润(单位:万元)为![]() 。
。
(1)求![]() 的分布列;
的分布列;
(2)求1件产品的平均利润(即![]() 的数学期望);
的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
(本小题满分13分)
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元。设1件产品的利润(单位:万元)为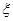 。
。
(1)求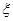 的分布列;
的分布列;
(2)求1件产品的平均利润(即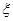 的数学期望);
的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
(本小题满分13分)
某产品按行业生产标准分成8个等级,等级系数X依次为1,2,……,8,其中X≥5为标准A,X≥3为标准B,已知甲厂执行标准A生产该产品,产品的零售价为6元/件;乙厂执行标准B生产该产品,产品的零售价为4元/件,假定甲、乙两厂得产品都符合相应的执行标准
(I)已知甲厂产品的等级系数X1的概率分布列如下所示:

且X1的数字期望EX1=6,求a,b的值;
(II)为分析乙厂产品的等级系数X2,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数X2的数学期望.
 在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
注:(1)产品的“性价比”= ;
;
(2)“性价比”大的产品更具可购买性.
(本小题满分13分)某工厂对一批产品的质量进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图.已知样本中产品净重小于100克的个数是36个。
(I)求样本中净重在 (克)的产品个数;
(克)的产品个数;
(II)若规定净重在 (克)的产品为一等品,依此抽样数据,求从该工厂随机抽取的3个产品中一等品个数
(克)的产品为一等品,依此抽样数据,求从该工厂随机抽取的3个产品中一等品个数 的分布列和数学期望.
的分布列和数学期望.

(本小题满分13分)
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),重量的分组区间为![]() ,
,
![]() ,. . . ,
,. . . ,![]() .由此得到样本的频率分布直方图,如图所示
.由此得到样本的频率分布直方图,如图所示
(Ⅰ)根据频率分布直方图,求重量超过505克的产品数量;
(Ⅱ)在上述抽取的40件产品中任取2件,设![]() 为重量超过505克的产品数量,求
为重量超过505克的产品数量,求![]() 的分布列;
的分布列;
(Ⅲ)从流水线上任取5件产品,估计其中恰有2件产品的重量超过505克的概率.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com