
题目列表(包括答案和解析)
(本题满分15分)已知函数![]()
![]() 且导数
且导数![]() .
.
(Ⅰ)试用含有![]() 的式子表示
的式子表示![]() ,并求
,并求![]() 单调区间; (II)对于函数图象上的不同两点
单调区间; (II)对于函数图象上的不同两点![]() ,如果在函数图象上存在点
,如果在函数图象上存在点![]() (其中
(其中![]() )使得点
)使得点![]() 处的切线
处的切线![]() ,则称
,则称![]() 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当![]() 时,又称
时,又称![]() 存在“中值伴侣切线”.试问:在函数
存在“中值伴侣切线”.试问:在函数![]() 上是否存在两点
上是否存在两点![]() 、
、![]() 使得它存在“中值伴侣切线”,若存在,求出
使得它存在“中值伴侣切线”,若存在,求出![]() 、
、![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(本题满分15分)已知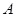 、
、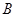 两点的坐标分别为A
两点的坐标分别为A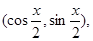 B
B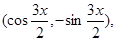
其中 。 (1)求
。 (1)求 的表达式;(2)若
的表达式;(2)若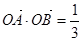 (
(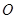 为坐标原点),求
为坐标原点),求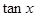 的值;
的值;
(3)若 (
(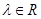 ),求函数
),求函数 的最小值。
的最小值。
(本题满分15分)已知三个函数![]()
其中第二个函数和第三个函数中的![]() 为同一个常数,且
为同一个常数,且![]() ,它们各自的最小值恰好是方程
,它们各自的最小值恰好是方程![]() 的三个根.
的三个根.
(Ⅰ) 求证:![]() ;
;
(Ⅱ) 设![]() 是函数
是函数![]() 的两个极值点,求
的两个极值点,求![]() 的取值范围.
的取值范围.
(本题满分15分)已知圆![]() :
:![]() ,一动直线l过
,一动直线l过![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 是
是![]() 中点,l与直线m:
中点,l与直线m:![]() 相交于
相交于![]() .
.
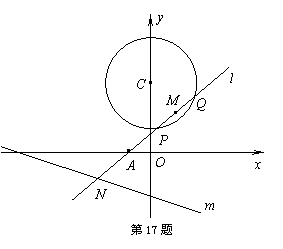 (Ⅰ)求证:当l与m垂直时,l必过圆心
(Ⅰ)求证:当l与m垂直时,l必过圆心![]() ;
;
(Ⅱ)当![]() 时,求直线l的方程;
时,求直线l的方程;
(Ⅲ)探索![]() 是否与直线l的倾斜角
是否与直线l的倾斜角
有关,若无关,请求出其值;若有关,
请说明理由.
(本题满分15分)已知三个函数![]()
其中第二个函数和第三个函数中的![]() 为同一个常数,且
为同一个常数,且![]() ,它们各自的最小值恰好是方程
,它们各自的最小值恰好是方程![]() 的三个根.
的三个根.
(Ⅰ) 求证:![]() ;
;
(Ⅱ) 设![]() 是函数
是函数![]() 的两个极值点,求
的两个极值点,求![]() 的取值范围.
的取值范围.
1-10.CDBBA CACBD
11..files/image037.gif) 12. ①③④ 13.-2或1 14.
12. ①③④ 13.-2或1 14. .files/image158.gif) 、
、.files/image282.gif) 15.2 16.
15.2 16. .files/image284.gif) 17.
17..files/image286.gif) .
.
18.
解:(1)由已知.files/image288.gif)
.files/image290.gif) 7分
7分
(2)由.files/image292.gif) 10分
10分
由余弦定理得.files/image294.gif) 14分
14分
19.(1)证明:∵PA⊥底面ABCD,BC.files/image296.gif) 平面AC,∴PA⊥BC,
3分
平面AC,∴PA⊥BC,
3分
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,∴BC⊥平面PAC. 5分
(2)解:过C作CE⊥AB于E,连接PE,
∵PA⊥底面ABCD,∴CE⊥面PAB,
∴直线PC与平面PAB所成的角为.files/image298.gif) , 10分
, 10分
∵AD=CD=1,∠ADC=60°,∴AC=1,PC=2,
.files/image300.gif) 中求得CE=
中求得CE=.files/image302.gif) ,∴
,∴.files/image304.gif) . 14分
. 14分
.files/image306.gif) 20.解:(1)由
20.解:(1)由.files/image235.gif) ①,得
①,得.files/image309.gif) ②,
②,
②-①得:.files/image310.gif) . 4分
. 4分
(2)由.files/image311.gif) 求得
求得.files/image313.gif) . 7分
. 7分
∴.files/image315.gif) ,
,.files/image317.gif) 11分
11分
.files/image319.gif)
∴.files/image321.gif) .
14分
.
14分
21.解:
(1)由.files/image252.gif) 得c=1 1分
得c=1 1分
.files/image323.gif) , 4分
, 4分
|