
题目列表(包括答案和解析)
C.选修4-4:坐标系与参数方程
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(1)求圆O和直线 的直角坐标方程;(2)当
的直角坐标方程;(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
D.选修4-5:不等式证明选讲
对于任意实数
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
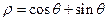 和直线
和直线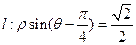 ,
, 的直角坐标方程;(2)当
的直角坐标方程;(2)当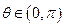 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
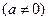 和
和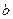 ,不等式
,不等式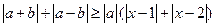 恒成立,试求实数
恒成立,试求实数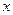 的取值范围.
的取值范围.C
[解析] 由基本不等式,得ab≤![]() =
=![]() =
=![]() -ab,所以ab≤
-ab,所以ab≤![]() ,故B错;
,故B错;![]() +
+![]() =
=![]() =
=![]() ≥4,故A错;由基本不等式得
≥4,故A错;由基本不等式得![]() ≤
≤![]() =
=![]() ,即
,即![]() +
+![]() ≤
≤![]() ,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×
,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =
=![]() ,故D错.故选C.
,故D错.故选C.
.定义域为R的函数 满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时, 的最小值为( )
的最小值为( )
(A) (B)
(B) (C)
(C) (D)
(D)
.过点 作圆
作圆 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( )
A.16条 B. 17条 C. 32条 D. 34条
说明:
一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则。
二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数。
四、只给整数分数,选择题和填空题不给中间分。
一、选择题:本大题共10小题,每小题5分,共50分。
1―5 BADBB 6―10 ACCDA
二、填空题:本大题共5小题,每小题4分,共20分。
11..files/image143.gif) 12.甲 13.7 14.
12.甲 13.7 14..files/image145.gif) 15.①③⑤
15.①③⑤
三、解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤。
16.解:.files/image147.gif) ……………………………………………………2分
……………………………………………………2分
.files/image149.gif) ………………………………………………………………4分
………………………………………………………………4分
.files/image151.gif)
.files/image153.gif)
.files/image155.gif) ………………………………………………………………6分
………………………………………………………………6分
.files/image157.gif) ………………………………………………9分
………………………………………………9分
.files/image159.gif) …………………………11分
…………………………11分
.files/image161.gif) ………………………………………………13分
………………………………………………13分
|