
题目列表(包括答案和解析)
| 2sinA | cosA+cos ( B-C ) |
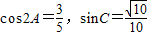 .
.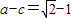 ,求a,b,c的值;
,求a,b,c的值;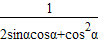 的值.
的值.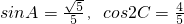 .
.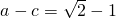 ,求a,b,c的值.
,求a,b,c的值.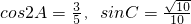 .
.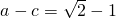 ,求a,b,c的值;
,求a,b,c的值;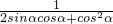 的值.
的值.| 2sinA |
| cosA+cos ( B-C ) |
一、选择题
1.B 2.C 3.C 4.C 5.B 6.A
7.A 8.D 9.B 10.D
二、填空题
11.86;1.6;12.1/6 13.( 4,8) 14.108 15.(1),(2),(3)
三、解答题
16.解:(1)由已知得 解得
解得 .设数列
.设数列 的公比为
的公比为 ,
,
由 ,可得
,可得 .又
.又 ,可知
,可知 ,
,
即 ,
,
解得 . 由题意得
. 由题意得 .
.  .
.
故数列 的通项为
的通项为 .……………………………6分
.……………………………6分
(2)由于 由(1)得
由(1)得


= ……………..13分
……………..13分
17.(1)∵ =a, AB=
=a, AB=
E为 的中点。
的中点。
∴ ,
,
DE⊥CE……(2分)
又∵ ∴DE⊥EB ,而
∴DE⊥EB ,而
∴DE⊥平面BCE…(6分)
(2) 取DC的中点F,则EF⊥平面BCD,作FH⊥BD于H,连EH,则∠EHF就是二面角E-BD-C的一个平面角。……………………(8分)
由题意得 EF=a,在Rt△ 中,
中, …………(10分)
…………(10分)
∴ ∠EHF=
∠EHF= .……………………………………………(13分)
.……………………………………………(13分)
18.解:由已知 ,
, 得
得 ,
,

(1)若 ,
, 。若A是直角,则k=-2;若B是直角,则
。若A是直角,则k=-2;若B是直角,则
k(2-k)+3=0, k=-1,k=3;若C是直角,则2(2-k)+12=0,k=8.故m=3,△ABC是直角三角形的概率为
(2)若 ,
, 且k≠
且k≠ .区间长度L=6.若B是钝角,则-k(2-k)-3<0, -1<k<3,L′=4. △ABC中B是钝角的概率
.区间长度L=6.若B是钝角,则-k(2-k)-3<0, -1<k<3,L′=4. △ABC中B是钝角的概率
k(2-k)+3=0, k=-1,k=3;若C是直角,则2(2-k)+12=0,k=8.故m=3,△ABC是直角三角形的概率为 .
.
求△ABC是直角三角形的概率.
19.解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以 为焦点,
为焦点,
长半轴为2的椭圆.它的短半轴 ,
,
故曲线C的方程为 .????????????????????????????????????????????????????????????????????????? 4分
.????????????????????????????????????????????????????????????????????????? 4分
(Ⅱ)设 ,其坐标满足
,其坐标满足
 消去y并整理得
消去y并整理得 ,
,
故 .??????????????????????????????????????????????????????????????????????? 6分
.??????????????????????????????????????????????????????????????????????? 6分
 ,即
,即 .而
.而 ,
,
于是 .
.
所以 时,
时, ,故
,故 .???????????????????????????????????????????????????????? 8分
.???????????????????????????????????????????????????????? 8分
当 时,
时, ,
, .
.
 ,
,
而
 ,
,
所以 . 13分
. 13分
20.解:(1)

 当
当 时
时 ,
,
函数 有一个零点;当
有一个零点;当 时,
时, ,函数
,函数 有两个零点。…….3分
有两个零点。…….3分
(2)假设 存在,由①知抛物线的对称轴为x=-1,∴
存在,由①知抛物线的对称轴为x=-1,∴ 即
即 
由②知对 ,都有
,都有
令 得
得


 又因为
又因为 恒成立,
恒成立,
 ,即
,即 ,即
,即
由 得
得 ,
,
当 时,
时, ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又
 对
对 ,都有
,都有 ,满足条件②。
,满足条件②。
∴存在 ,使
,使 同时满足条件①、②。…..8分
同时满足条件①、②。…..8分
(3)令 ,则
,则

 ,
,

 在
在 内必有一个实根。即
内必有一个实根。即 ,使
,使 成立。….13分
成立。….13分
21.(1)1; (2) 
(2)(1)设M= ,则有
,则有
 =
= ,
,
 =
= ,
,
所以 且
且 解得
解得 ,所以M=
,所以M= .…………………………5分
.…………………………5分
(2)任取直线l上一点P(x,y)经矩阵M变换后为点P’(x’,y’).
因为 ,所以又m:
,所以又m: ,
,
所以直线l的方程(x+2y)-(3x+4y)=4,即x+y+2=0.………………………………7分
.
不等式证明选讲)若 ,证明
,证明 。
。
柯西不等式一步可得
www.ks5u.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com