练习册

  • 练习册
  • 试题
    13．按照某学者的理论.假设一个人生产某产品的单件成本为a元.如果他卖出该产品的单价为m元.则他的满意度为,如果他买进该产品的单价为n元.则他的满意度为.如果一个人对两种交易的满意度分别为h1和h2.则他对这两种交易的综合满意度为. 现假设甲生产A.B两种产品的单件成本分别为12元和5元.乙生产A.B两种产品的单件成本分别为3元和20元．设产品A.B的单价分别为mA元和mB元.甲买进A与卖出B的综合满意度为h甲.乙卖出A与买进B的综合满意度为h乙． (1)求h甲和h乙关于mA.mB的表达式,当mA＝mB时.求证:h甲＝h乙, (2)设mA＝mB.当mA.mB分别为多少时.甲.乙两人的综合满意度均最大?最大的综合满意度为多少? 中最大的综合满意度为h0.试问能否适当选取mA.mB的值.使得h甲≥h0和h乙≥h0同时成立.但等号不同时成立?试说明理由． 解:设mA＝x.mB＝y. (1)甲买进产品A的满意度:h1甲＝,甲卖出产品B的满意度:h2甲＝, 甲买进产品A和卖出产品B的综合满意度: h甲＝, 同理.乙卖出产品A和买进产品B的综合满意度: h乙＝. 当x＝y时.h甲＝＝＝.h乙＝＝＝. 故h甲＝h乙． (2)当x＝y时.由(1)知h甲＝h乙＝. 因为＝≤.且等号成立当且仅当y＝10. 当y＝10时.x＝6. 因此.当mA＝6.mB＝10时.甲.乙两人的综合满意度均最大.且最大的综合满意度为. 知h0＝. 因为h甲h乙＝ ＝≤. 所以.当h甲≥.h乙≥时.有h甲＝h乙＝. 因此.不能取到mA.mB的值.使得h甲≥h0和h乙≥h0同时成立.但等号不同时成立． 【查看更多】

     

    题目列表(包括答案和解析)

    (本小题满分20分)在金融危机中,某钢材公司积压了部分圆钢,经清理知共有2009根.现将它们堆放在一起.

    (1)若堆放成纵断面为正三角形(每一层的根数比上一层根数多1根),并使剩余的圆钢尽可能地少,则剩余了多少根圆钢?

    (2)若堆成纵断面为等腰梯形(每一层的根数比上一层根数多1根),且不少于七层，

    （Ⅰ）共有几种不同的方案?

    （Ⅱ）已知每根圆钢的直径为10cm，为考虑安全隐患，堆放高度不得高于4m，则选择哪个方案，最能节省堆放场地？

    查看答案和解析>>

    （2009•红桥区二模）某中学对高一新入学的两个班同学进行测试，满分100分，80分以上为优秀，现将两个班学生的成绩整理后分成五组，绘制频率分布直方图，已知图中从左到右的第一、第三、第四、第五小组频率分别为0.05、0.30、0.20、0.05．第二小组频数为32，则参赛的人数和优秀率分别为（　　）

    查看答案和解析>>

    （2009•温州一模）已知某班级有女生20人，男生30人．一次考试女生的平均分为75分，全班的平均分为72分，则男生的平均分为
    70分
    70分
    ．

    查看答案和解析>>

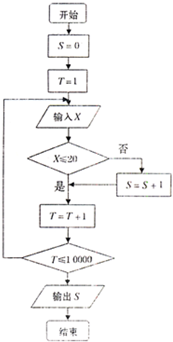    （2009•枣庄一模）为调查某市中学生平均每人每天参加体育锻炼时间X（单位：分钟），按锻炼时间分下列四种情况统计：①0～10分钟；②11～20分钟；③21～30分钟；④30分钟以上，有10000名中学生参加了此项活动，如图是此次调查中某一项的流程图，若平均每天参加体育锻炼的时间在0～20分钟的学生的频率是0.15，则输出的结果为
    8500
    8500
    ．

    查看答案和解析>>

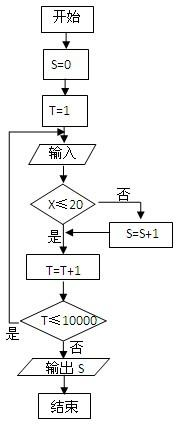    我市某机构为调查2009年下半年落实中学生“阳光体育”活动的情况，设平均每人每天参加体育锻炼时间为X（单位：分钟），按锻炼时间分下列四种情况统计：①0～10分钟；②11～20分钟；③21～30分钟；④30分钟以上，有10000名中学生参加了此项活动，右图是此次调查中某一项的流程图，其输出的结果是6200，则平均每天参加体育锻炼时间在0～20分钟内的学生的频率是（　　）

    查看答案和解析>>


    同步练习册答案