
题目列表(包括答案和解析)
(本小题满分12分)
已知函数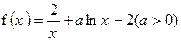
(Ⅰ)若曲线y=f(x)在点P(1,f(1))处的切线与直线 y=x+2垂直,求函数y=f(x)的单调区间;[来源:学&科&网Z&X&X&K]
y=x+2垂直,求函数y=f(x)的单调区间;[来源:学&科&网Z&X&X&K]
(Ⅱ)若对于任意 成立,试求a的取值范围;
成立,试求a的取值范围;
(Ⅲ)记g(x)=f(x)+x-b(b∈R).当a=1时,函数g(x)在区间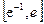 上有两个零点,求实数b的取值范围。
上有两个零点,求实数b的取值范围。
(本小题满分12分)
已知函数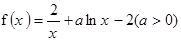
(Ⅰ)若曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直,求函数y=f(x)的单调区间;[来源:学&科&网Z&X&X&K]
(Ⅱ)若对于任意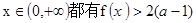 成立,试求a的取值范围;
成立,试求a的取值范围;
(Ⅲ)记g(x)=f(x)+x-b(b∈R).当a=1时,函数g(x)在区间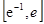 上有两个零点,求实数b的取值范围。
上有两个零点,求实数b的取值范围。
(本小题满分12分)
已知函数f (x)=alnx+x2 (a为实常数).[来源:ZXXK][来源:学*科*网Z*X*X*K]
(Ⅰ)若a=-2,求证:函数f (x)在(1,+∞)上是增函数;
(Ⅱ)求函数f (x)在[1,e]上的最小值及相应的x值;
(Ⅲ)若当x∈[1,e]时,f (x)≤(a+2)x恒成立,求实数a的取值范围.
(本小题满分12分)
阅读下面内容,思考后做两道小题。
在一节数学课上,老师给出一道题,让同学们先解,题目是这样的:
已知函数f(x)=kx+b,1≤f(1)≤3,-1≤f(-1)≤1,求Z=f(2)的取值范围。
题目给出后,同学们马上投入紧张的解答中,结果很快出来了,大家解出的结果有很多个,下面是其中甲、乙两个同学的解法:
甲同学的解法:由f(1)=k+b,f(-1)=-k+b得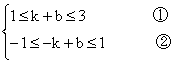
①+②得:0≤2b≤4,即0≤b≤2 ③
② ×(-1)+①得:-1≤k-b≤1 ④
④+②得:0≤2k≤4 ⑤
③+⑤得:0≤2k+b≤6。
又∵f(2)=2k+b
∴0≤f(2)≤6,0≤Z≤6
乙同学的解法是:由f(1)=k+b,f(-1)=-k+b得
①+②得:0≤2b≤4,即:0≤b≤2 ③
①-②得:2≤2k≤2,即:1≤k≤1
∴k=1,
∵f(2)=2k+b=1+b
由③得:1≤f(2)≤3
∴:1≤Z≤3
(Ⅰ)如果课堂上老师让你对甲、乙两同学的解法给以评价,你如何评价?
(Ⅱ)请你利用线性规划方面的知识,再写出一种解法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com