20090325
又(09.3).files/image144.gif)
则(09.3).files/image146.gif) …………4分
…………4分
(II)由余弦定理得(09.3).files/image148.gif)
(09.3).files/image150.gif)
所以(09.3).files/image152.gif) 时等号成立…………9分
时等号成立…………9分
所以(09.3).files/image154.gif) …………10分
…………10分
18.(本小题满分12分)
解:(I)解:由已知条件得
(09.3).files/image156.gif) …………2分
…………2分
即(09.3).files/image158.gif) …………6分
…………6分
答:(09.3).files/image160.gif)
(II)解:设至少有两量车被堵的事件为A…………7分
则(09.3).files/image162.gif) …………12分
…………12分
答:至少有两量车被堵的概率为(09.3).files/image164.gif)
19.(本题满分12分)
解:(法一)
(I)DF//BC,(09.3).files/image166.gif)
(09.3).files/image168.gif)
(09.3).files/image170.gif) 平面ACC1A1
平面ACC1A1
(09.3).files/image172.gif) …………2分
…………2分
(09.3).files/image174.gif)
(09.3).files/image176.gif) …………4分
…………4分
(II)(09.3).files/image178.gif)
(09.3).files/image180.gif) 点B1到平面DEF的距离等于点C1到平面DEF的距离
点B1到平面DEF的距离等于点C1到平面DEF的距离
(09.3).files/image182.gif)
(09.3).files/image184.gif)
设(09.3).files/image186.gif) 就是点C1到平面DEF的距离…………6分
就是点C1到平面DEF的距离…………6分
由题设计算,得(09.3).files/image188.gif) …………8分
…………8分
(III)作(09.3).files/image190.gif) 于M,连接EM,因为
于M,连接EM,因为(09.3).files/image192.gif) 平面ADF,
平面ADF,
所以(09.3).files/image194.gif) 为所求二面角的平面角。
为所求二面角的平面角。
则(09.3).files/image196.gif)
则M为AC中点,即M,D重合,…………10分
则(09.3).files/image198.gif) ,所以FD与BC平行,
,所以FD与BC平行,
所以F为AB中点,即(09.3).files/image200.gif) …………12分
…………12分
(法二)解:以C点为坐标原点,CA所在直线为(09.3).files/image202.gif) 轴,CB所在直线为
轴,CB所在直线为(09.3).files/image204.gif) 轴,CC1所在直线为z轴建立空间直角坐标系…………1分
轴,CC1所在直线为z轴建立空间直角坐标系…………1分
(1)由(09.3).files/image206.gif)
(09.3).files/image208.jpg)
(09.3).files/image212.gif) (09.3).files/image214.gif) …………4分 …………4分 (II)(09.3).files/image216.gif) (09.3).files/image218.gif) 又(09.3).files/image220.gif) …………6分 …………6分 (09.3).files/image222.gif) …………8分 …………8分 (III)设(09.3).files/image224.gif) ,平面DEF的法向量 ,平面DEF的法向量 (09.3).files/image226.gif) …………10分 …………10分 (09.3).files/image228.gif) (09.3).files/image230.gif) 即F为线段AB的中点, 即F为线段AB的中点, (09.3).files/image232.gif) …………12分 …………12分 20.(本题满分12分) 解:(I)由(09.3).files/image234.gif) (09.3).files/image236.gif) (09.3).files/image238.gif) …………6分 …………6分 (II)由(09.3).files/image234.gif) 得(09.3).files/image241.gif) (09.3).files/image243.gif) (09.3).files/image245.gif) 是等差数列;…………10分 是等差数列;…………10分 (09.3).files/image247.gif) (09.3).files/image249.gif) (09.3).files/image251.gif) …………12分 …………12分 21.(本题满分12分) 解:(I)(09.3).files/image253.gif) …………2分 …………2分 又(09.3).files/image255.gif) …………4分 …………4分 (II)(09.3).files/image257.gif) (09.3).files/image259.gif) 且(09.3).files/image261.gif) (09.3).files/image263.gif) …………8分 …………8分 (09.3).files/image265.gif) (09.3).files/image267.gif) …………12分 …………12分 22.(本题满分12分) 解:(1)A1(-1,0),A2(1,0),F1(-2,0),F2(2,0) (09.3).files/image269.gif) (09.3).files/image271.gif) (09.3).files/image273.gif) …………4分 …………4分 (II)设(09.3).files/image275.gif) 直线PF1与双曲线交于(09.3).files/image277.gif) 直线PF2与双曲线交于(09.3).files/image279.gif) (09.3).files/image281.gif) 令(09.3).files/image283.gif) (09.3).files/image285.gif) (09.3).files/image287.gif) …………6分 …………6分 (09.3).files/image289.gif) 而(09.3).files/image291.gif) (09.3).files/image180.gif) 直线PF1与双曲线交于两支上的两点, 直线PF1与双曲线交于两支上的两点, 同理直线PF2与双曲线交于两支上的两点 则(09.3).files/image294.gif) …………8分 …………8分 (09.3).files/image296.gif) (09.3).files/image298.gif) …………10分 …………10分 解得(09.3).files/image300.gif)
| |

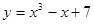 上,则该曲线在点P处的切线的倾斜角的取值范围是
( )
上,则该曲线在点P处的切线的倾斜角的取值范围是
( )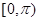 B.
B.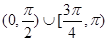
 D.
D.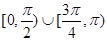
![]() )∪[
)∪[![]() ,π)
,π)![]()
![]()
(09.3).files/image138.gif)
(09.3).files/image140.gif)