
题目列表(包括答案和解析)
| OM |
| OA |
| ON |
| OB |
| x |
| x+1 |
| x |
| x+1 |
| 1 |
| f(x) |
| 1 |
| 2 |
| OP |
| OP1 |
| OP2 |
| OPn |
| OP |
| OQ |
| 1 |
| 2 |
| OM |
| OA |
| ON |
| OB |
| x |
| x+1 |
| x |
| x+1 |
| 1 |
| f(x) |
| 1 |
| 2 |
| OP |
| OP1 |
| OP2 |
| OPn |
| OP |
| OQ |
| 1 |
| 2 |
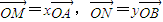 .
.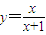 ;
;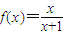 ,定义函数
,定义函数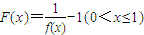 ,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为 的等比数列,O为原点,令
的等比数列,O为原点,令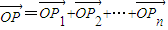 ,是否存在点Q(1,m),使得
,是否存在点Q(1,m),使得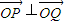 ?若存在,请求出Q点坐标;若不存在,请说明理由.
?若存在,请求出Q点坐标;若不存在,请说明理由.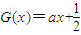 在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.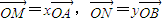 .
.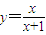 ;
;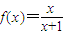 ,定义函数
,定义函数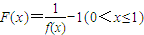 ,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为 的等比数列,O为原点,令
的等比数列,O为原点,令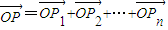 ,是否存在点Q(1,m),使得
,是否存在点Q(1,m),使得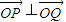 ?若存在,请求出Q点坐标;若不存在,请说明理由.
?若存在,请求出Q点坐标;若不存在,请说明理由.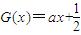 在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.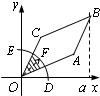 8、如图,圆弧型声波DFE从坐标原点O向外传播.若D是DFE弧与x轴的交点,设OD=x(0≤x≤a),圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为y(图中阴影部分),则函数y=f(x)的图象大致是( )
8、如图,圆弧型声波DFE从坐标原点O向外传播.若D是DFE弧与x轴的交点,设OD=x(0≤x≤a),圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为y(图中阴影部分),则函数y=f(x)的图象大致是( )
一、选择题:
1―6DABADD 7―12DCABBB
二、填空题:
13.-10
14.(09.3).files/image138.gif)
15.4
16.①②⑤
三、解答题:
17.(本题满分10分)
解:(I)由向量(09.3).files/image140.gif)
|