
题目列表(包括答案和解析)
(本小题满分12分)在第9届校园文化艺术节棋类比赛项目报名过程中,我校高二(2)班共有16名男生和14名女生预报名参加,调查发现,男、女选手中分别有10人和6人会围棋.
(I)根据以上数据完成以下2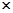 2列联表:
2列联表:
|
|
会围棋 |
不会围棋 |
总计 |
|
男 |
|
|
|
|
女 |
|
|
|
|
总计 |
|
|
30 |
并回答能否在犯错的概率不超过0.10的前提下认为性别与会围棋有关?
参考公式: 其中n=a+b+c+d
其中n=a+b+c+d
参考数据:
|
|
0.40 |
0.25 |
0.10 |
0.010 |
|
|
0.708 |
1.323 |
2.706 |
6.635 |
(Ⅱ)若从会围棋的选手中随机抽取3人成立该班围棋代表队,则该代表队中既有男又
有女的概率是多少?
(Ⅲ)若从14名女棋手中随机抽取2人参加棋类比赛,记会围棋的人数为 ,求
,求 的期望.
的期望.
(本小题满分12分)
已知斜三棱柱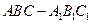 ,
,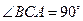 ,
, ,
,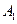 在底面
在底面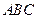 上的射影恰
上的射影恰
为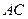 的中点
的中点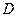 ,
,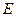 为
为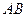 的中点,
的中点,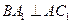 .
.
(I)求证: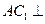 平面
平面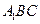 ;
;
(II)求二面角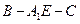 余弦值的大小.
余弦值的大小.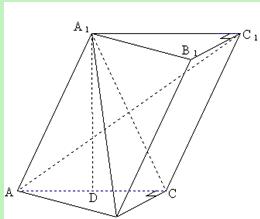
(本小题满分12分)
三角形的三个内角A、B、C所对边的长分别为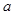 、
、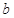 、
、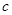 ,设向量
,设向量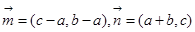 ,若
,若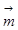 //
//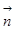 .
.
(I)求角B的大小;
(II)求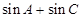 的取值范围.
的取值范围.
(本小题满分12分)
某校高三年级要从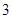 名男生
名男生 和
和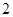 名女生
名女生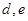 中任选
中任选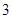 名代表参加学校的演讲比赛。
名代表参加学校的演讲比赛。
(I)求男生 被选中的概率
被选中的概率
(II)求男生 和女生
和女生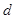 至少一人被选中的概率。
至少一人被选中的概率。
(本小题满分12分)已知△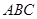 三内角满足
三内角满足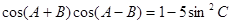 ,
,
(1)证明: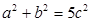 ;
;
(2)求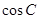 的最小值.
的最小值.
一、选择题:
1―6DABADD 7―12DCABBB
二、填空题:
13.-10
14.(09.3).files/image138.gif)
15.4
16.①②⑤
三、解答题:
17.(本题满分10分)
解:(I)由向量(09.3).files/image140.gif)
|