如图11，在直角梯形中，∥，，点为坐标原点，点在轴的正半轴上，对角线，相交于点，，．

（1）线段的长为            ，点的坐标为              ；

（2）求△的面积；

（3）求过，，三点的抛物线的解析式；

（4）若点在（3）的抛物线的对称轴上，点为该抛物线上的点，且以，，，四点为顶点的四边形为平行四边形，求点的坐标．

如图11所示，在梯形ABCD中，已知AB∥CD， AD⊥DB，AD=DC=CB，AB=4．以AB所在直线为轴，过D且垂直于AB的直线为轴建立平面直角坐标系．

（1）求∠DAB的度数及A、D、C三点的坐标；

（2）求过A、D、C三点的抛物线的解析式及其对称轴L．

（3）若P是抛物线的对称轴L上的点，那么使PDB为等腰三角形的点P有几个?（不必求点P的坐标，只需说明理由）

如图11，直线与y轴交于A点，与反比例函数（x＞0）的图象交

      于点M，过M作MH⊥x轴于点H，且tan∠AHO＝2.

（1）求k的值；

（2）点N（a，1）是反比例函数（x＞0）图像上的点，

在x轴上是否存在点P，使得PM＋PN最小，若存

在，求出点P的坐标；若不存在，请说明理由.

如图11-1，是我们平时使用的等臂圆规，即CA=CB．若n个相同规格的等臂圆规的两脚依次摆放在同一条直线上如图2所示，其张角度数变化如下：∠A₁C₁A₂=160°，∠A₂C₂A₃=80°，∠A₃C₃A₄=40°，∠A₄C₄A₅=20°，…. ，根据上述规律请你写出∠A_nC_nA_n+1=_______________°．（用含n的代数式表示）

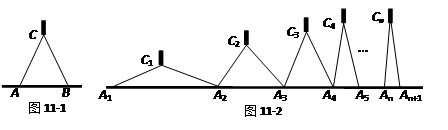
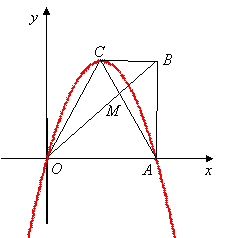
如图11，已知○为坐标原点，∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).

1.求点B的坐标

2.若二次函数y=ax+bx+c的图象经过A、B、O三点，求此二次函数的解析式；

3.在(2)中的二次函数图象的OB段(不包括点O、B)上，是否存在一点C，使得四边形ABCO的面积最大？若存在，求出这个最大值及此时点C的坐标；若不存在，请说明理由。