
题目列表(包括答案和解析)
解:(1)如图①AH=AB
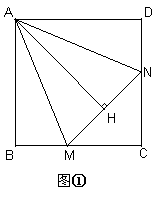 (2)数量关系成立.如图②,延长CB至E,使BE=DN
(2)数量关系成立.如图②,延长CB至E,使BE=DN
∵ABCD是正方形
∴AB=AD,∠D=∠ABE=90°
∴Rt△AEB≌Rt△AND
∴AE=AN,∠EAB=∠NAD
∴∠EAM=∠NAM=45°
∵AM=AM
∴△AEM≌△ANM
∵AB、AH是△AEM和△ANM对应边上的高,
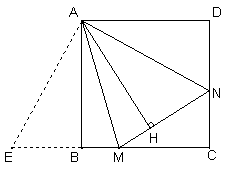 ∴AB=AH
∴AB=AH
(3)如图③分别沿AM、AN翻折△AMH和△ANH,
得到△ABM和△AND
∴BM=2,DN=3,∠B=∠D=∠BAD=90°
分别延长BM和DN交于点C,得正方形ABCE.
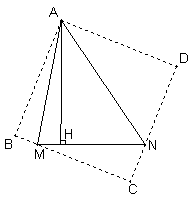 由(2)可知,AH=AB=BC=CD=AD.
由(2)可知,AH=AB=BC=CD=AD.
设AH=x,则MC=![]() , NC=
, NC=![]() 图②
图②
在Rt⊿MCN中,由勾股定理,得
![]()
∴![]()
解得![]() .(不符合题意,舍去)
.(不符合题意,舍去)
∴AH=6.
解:(1)A(-1,0),B(3,0),C(0,3).·················· 2分
抛物线的对称轴是:x=1.······················· 3分
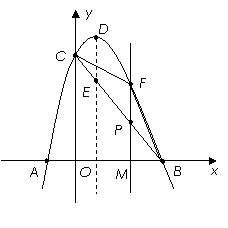 (2)①设直线BC的函数关系式为:y=kx+b.
(2)①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得:
![]() 解得:k= -1,b=3.
解得:k= -1,b=3.
所以直线BC的函数关系式为:![]() .
.
当x=1时,y= -1+3=2,∴E(1,2).
当![]() 时,
时,![]() ,
,
∴P(m,![]() m+3).·························· 4分
m+3).·························· 4分
在![]() 中,当
中,当![]() 时,
时,![]()
∴![]()
当![]() 时,
时,![]() ∴
∴![]() ········· 5分
········· 5分
∴线段DE=4-2=2,线段![]() ···· 6分
···· 6分
∵![]()
∴当![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
由![]() 解得:
解得:![]() (不合题意,舍去).
(不合题意,舍去).
因此,当![]() 时,四边形
时,四边形![]() 为平行四边形.··········· 7分
为平行四边形.··········· 7分
②设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,由
,由![]() 可得:
可得:![]()
∵![]() ························ 8分
························ 8分
即![]() .
.
![]()
![]() ·········· 9分
·········· 9分
解:(1)△AFB∽△FEC.
证明:由题意得:∠AFE=∠D=90° 又∠B=∠C=90°
∴∠BAF+∠AFB=90° , ∠EFC+∠AFB=90°
∴∠BAF=∠EFC ∴ AFB∽△FEC
(2)设EC=3x,FC=4x,则有DE=EF=5x ,∴AB=CD=3x+ 5x=8x
由△AFB∽△FEC得:![]() 即:
即:![]() =
=![]() ∴BF=6x ∴BC=BF-CF=6x+ 4x= 10x
∴BF=6x ∴BC=BF-CF=6x+ 4x= 10x
∴在Rt△ADE中,AD=BC=10x,AE=![]() ,则有
,则有![]()
解得![]() (
(![]() 舍去) ∴AB+BC+CD+DA=36x=36(cm) 答:矩形ABCD的周长为36cm.
舍去) ∴AB+BC+CD+DA=36x=36(cm) 答:矩形ABCD的周长为36cm.
阅读下列例题:解方程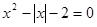
(1)当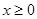 时,原方程化为
时,原方程化为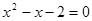 ,解之得
,解之得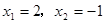 (不符题意,舍去)
(不符题意,舍去)
(2)当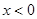 时,原方程化为
时,原方程化为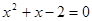 ,解之得
,解之得 (不符题意,舍去)
(不符题意,舍去)
所以原方程的解是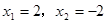
请参照例题解方程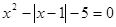 .
.
阅读下列例题:解方程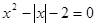
(1)当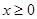 时,原方程化为
时,原方程化为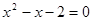 ,解之得
,解之得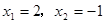 (不符题意,舍去)
(不符题意,舍去)
(2)当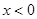 时,原方程化为
时,原方程化为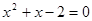 ,解之得
,解之得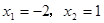 (不符题意,舍去)
(不符题意,舍去)
所以原方程的解是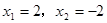
请参照例题解方程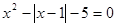 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com