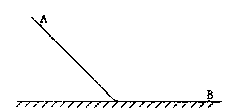
（07年沈阳地区期中）(9分)某研究性学习小组的同学们欲根据所学力学知识测量物体与某种材料间的动摩擦因数μ。为避免速度的测量，他们采取以下方案：将这种材料铺设于如左下图所示的斜而轨道与水平轨道上，两轨道接触处有一小段弧形轨道以保证变轨道时不损失速度，整个装置放于水平面上。将小物体自斜面上A点静止起释放，发现最终物体停在水平轨道上B点。通过一些必要的测量，他们便解决了问题。思考后请回答以下问题：（注：当地的重力加速度g未知）

        （1）在以下给出的器材中选出合适的来完成本实验            （填序号即可）

          ①刻度尺  ②量角器  ③秒表  ④天平  ⑤铅垂线  ⑥白纸及铅笔等文具

（2）根据所选实验器材，写出需要测量的物理量             （表述要准确地位，指明物理量的符号）。

（3）根据测量的物理量，写出计算动摩擦因数μ的表达式           （用物理量的符号表示）。