
题目列表(包括答案和解析)
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
|
销售经验(年) |
1 |
3 |
4 |
4 |
6 |
8 |
10 |
10 |
11 |
13 |
|
年销售额(千元) |
80 |
97 |
92 |
102 |
103 |
111 |
119 |
123 |
117 |
136 |
(1)依据这些数据画出散点图并作直线 =78+4.2x,计算
=78+4.2x,计算 (yi-
(yi- i)2;
i)2;
(2)依据这些数据由最小二乘法求线性回归方程,并据此计算 ;
;
(3)比较(1)和(2)中的残差平方和 的大小.
的大小.
|
| α |
|
| β |
|
| π |
| 4 |
| ||
| 2 |
|
若方程x2+(m-2)x-m+5=0的两个根都大于2,求实数m的取值范围.
阅读下面的解法,回答提出的问题.
解:第一步,令判别式Δ=(m-2)2-4(-m+5)≥0,
解得m≥4或m≤-4;
第二步,设两根为x1,x2,由x1>2,x2>2得
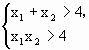 ,所以
,所以![]() .
.
所以m<-2.
第三步,由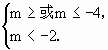 得m≤-4.
得m≤-4.
第四步,由第三步得出结论.
当m∈(-∞,-4]时,此方程两根均大于2.
但当取m=-6检验知,方程x2-8x+11=0两根为x=4±![]() ,其中4-
,其中4-![]() <2.
<2.
试问:产生错误的原因是什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com